Поскольку размеры сечения могут быть любыми, используем метод последовательных приближений. Выполним первое приближение. Примем 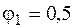 . Из условия устойчивости (6.6) найдем площадь сечения, подставив
. Из условия устойчивости (6.6) найдем площадь сечения, подставив 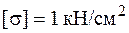 :
:
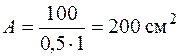 .
.
Поскольку 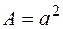 , то
, то 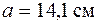 . Найдем минимальный радиус инерции сечения. Для квадрата любая ось является главной и радиус инерции относительно любой оси
. Найдем минимальный радиус инерции сечения. Для квадрата любая ось является главной и радиус инерции относительно любой оси
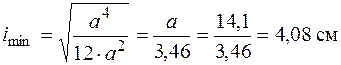 .
.
Зная радиус инерции, вычислим гибкость стержня по формуле (6.1):
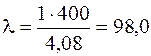 .
.
По таблице находим для дерева 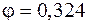 . Полученное значение
. Полученное значение 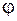 еще сильно отличатся от величины
еще сильно отличатся от величины 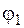 , принятой в начале первого приближения, поэтому выполним второе приближение. Найдем
, принятой в начале первого приближения, поэтому выполним второе приближение. Найдем 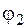 как среднее арифметическое между
как среднее арифметическое между 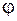 и
и 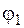 :
:

и повторим все действия, выполненные в первом приближении:
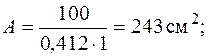
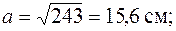
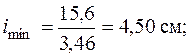
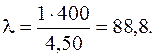
Этой гибкости соответствует 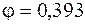 . Выполним еще одно, третье, приближение:
. Выполним еще одно, третье, приближение:
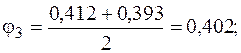
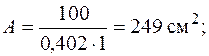
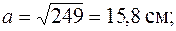
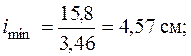
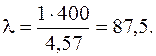
Соответствующее этой гибкости значение 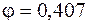 отличается от
отличается от 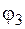 на 1,2 %. Такая точность достаточна, поэтому примем
на 1,2 %. Такая точность достаточна, поэтому примем 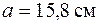 . Для этого размера в условии устойчивости
. Для этого размера в условии устойчивости
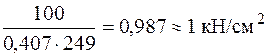
достигнуто желаемое равенство.
В заключение проверим условие прочности, считая 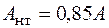 .
.
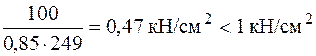 .
.
 2015-01-30
2015-01-30 555
555







