Билет №22.Равномерное распределение.Параметры распределения,числовые характеристики

Непреры́вное равноме́рное распределе́ние — в теории вероятностей - распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна. Случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где a,b€ R

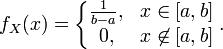
Функция распр.

Интегрируя определённую выше плотность, получаем: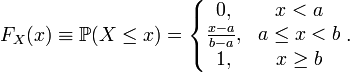

Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b]\!, то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

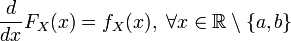
Билет №23.Показательное распределение.Параметры распределения,числовые характеристики.

Показательное распределение-непрерывное распределение вероятностей случайной величины X, задаваемое плотностью

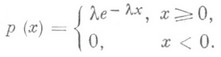
Плотность р(х).зависит от положительного масштабного параметра l. Формула для моментов: 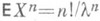в частности - для математич. Ожидания 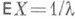, дисперсии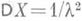

характеристич. функция: (1-it/l)-1.

П. р. входит в семейство распределений, называемых гамма-распределениями и задаваемых плотностью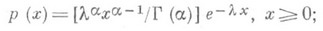

Билет №24.Нормальное распределение.Параметры распределния,числовые хар-ки.Правило трех сигм,Стандартное нормальное распределение.Связь нормального распределения общего вида со стандартным норм распределением

Нормальное распределение,также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса: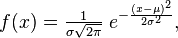

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ — стандартное отклонение (σ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.

Значение:

Важное значение нормального распределения во многих областях науки, например, в математической статистике и статистической физике вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.

Свойства:

Моментами и абсолютными моментами случайной величины X называются математические ожидания Xp и 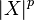соответственно. Если математическое ожидание случайной величины μ = 0, то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых p.

Если 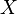имеет нормальное распределение, то для неё существуют (конечные) моменты при всех 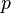с действительной частью больше −1. Для неотрицательных целых p, центральные моменты таковы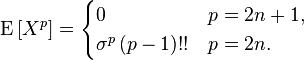

Здесь 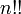означает двойной факториал, то есть произведение всех нечетных от n до 1.

Центральные абсолютные моменты для неотрицательных целых p таковы:

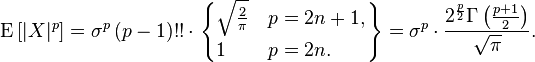
Последняя формула справедлива также для произвольных p > -1.

Правило трех сигм

Правило трёх сигм(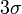)— практически все значения нормально распределённой случайной величины лежат в интервале 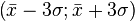Более строго — приблизительно с 99,73 % вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина 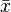истинная, а не полученная в результате обработки выборки).

Если же истинная величина 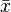неизвестна, то следует пользоваться не 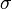,а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.

Билет №25.Закон больших чисел.Лемма о среднем арифметическом случайных величин.Теорема Бернулли.Центральная предельная теорема.

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое конечное число испытаний, при котором с любой заданной наперёд вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.