Теорема сложения вероятностей. Условная вероятность. Теорема умножения вероятностей

Билет 5
Формула полной вероятности. Формула Байеса.

Биномиальная схема испытаний. Формула Бернулли, наиболее вероятное число успехов.

Теорема(формула Бернулли). Обозначим через Pn(m) вероятность того, что событие А наступило m раз в n испытаниях. Вероятность Pn(m) определяется формулой

Pn(m) = C_n^m *p^m *qⁿ^-^m

Определение. Число наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число m0 наступлений события А в n испытаниях заключено в интервале np - q <= m₀ <=np + p Если np- q −целое число, то наивероятнейших числа два np - q и np+ p.

Приближенные формулы Муавра-Лапласа и Пуассона.

Предположим, что мы хотим вычислить вероятность Pn (m) появления события A при большом числе испытаний n. Ясно, что в этом случае непосредственное вычисление по формуле Бернулли технически сложно, тем более, если учесть, что сами p и q – числа дробные. Поэтому возникает естественное желание иметь более простые, пусть даже и приближенные, формулы для вычисления Pn (m) при больших n.

Наиболее известными являются формулы Пуассона и Муавра- Лапласа.

Теорема Муавра-Лапласа (локальная). Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Pn (m), того, что в n испытаниях события А наступит m раз, приближенно равна

P= (1/√(npq))*φ(x), где x=(m-np)/√(npq), а функция φ – функция Гаусса(см. в таблице значений) ϕ(x) является четной, ϕ(x) –монотонно убывающая при положительных значениях x и при x>4 функция приближенно равна 0.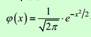

Теорема Муавра-Лапласа (интегральная). Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n испытаниях число успехов m находится между m1 и m2 приближенно равна

P(m1<m<m2)=1/2(Ф(x2) – Ф(x1)), где x_i = (m_i-np)/√(npq) и i=1,2. 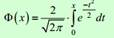нечетная функция.

Теорема (Пуассона). Предположим, что произведение np остается постоянной величиной, когда n неограниченно возрастает. Обозначим λ = np. Тогда для любого фиксированного m и любого постоянного λ:

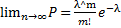
В случае, когда n велико (n >100), а р мало (p < 0,1), причем npq ≤ 9, вместо формулы Бернулли применяют приближенную формулу Пуассона

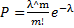, Где λ = np.

Случайные величины. Типы случайных величин, закон распределения дискретной случайной величины. Независимость случайных величин.

Определение: Функция, заданная в пространстве элементарных событий Ω ={ 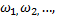} Называется случайной величиной. Очевидно, что значение случайной величины x_i наступает с вероятностью p_i, равной вероятности наступления соотв. События ω_i.

Соответствие, которое каждому зачению величины x_i дискретной случайной величины X сопоставляет его с вероятностью p_i и называется законом распределения случайной величины X. Его можно задать таблично, аналитически (в виде формулы) и графически. Дискретную случайную величину задаёт ряд распределения – это таблица, в которой перечислены все возможные значения дискретной случайной величины и соответствующие им вероятности

События X=x1,… составляют такую группу, что сумма их ероятностей равна 1.

Две случайные величины X Y, называются независимыми, если вероятность совместного появления событий равна произведению вероятностей P = ({X = a} * {Y = b} = P ({X = a})* P({Y = b}) Арифметические операции над дискретными случайными величинами.

Произведением kX случайной величины X на постоянное число k называется случайная величина, которая с теми же вероятностями, что и X принимает новые значения, равные, 1,..., i kx i n =. Таким образом, закон распределения для новой случайной величины kX имеет вид:

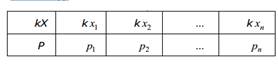
Пусть Y ─ еще одна дискретная СВ: Сумма Z = X+Y = двух случайных величин ─ это новая случайная величина, которая принимает все значения вида z_i = x_i + y_j с вероятностями p_k₌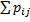

Произведением Z= X*Y = ⋅ называется новая случайная величина, принимающая все значения вида z_i = x_i *y_j_.

Квадрат случайной величины X ─ это новая случайная величина, которая с теми же вероятностями, что и X принимает значения x_i².

Математическое ожидание случайной величины. Свойства математического ожидания.

Пусть случайная величина Х может принимать только значения x_1,x₂,…x_n вероятности которых соответственно равны p_1,p₂,…p_n. Тогда математическое ожидание М (Х) случайной величины Х определяется равенством 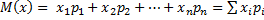. Из определения следует, что математическое ожидание дискретной случайной величины есть величина неслучайная. Св-ва: 1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C;

2. Постоянный множитель можно выносить за знак математического ожидания: M (CX) = CM(X)

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий M (XY) = M(X)*M(Y)

5. Математическое ожидание отклонения случайной величины от ее математического ожидания

равно нулю: M(X – M(X))=0

Дисперсия случайной величины. Свойства дисперсии.

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Дисперсией D (X) случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D (X) = M [X – M(X)]². Если Х – дискретная случайная величина, то дисперсию вычисляют по следующим формулам:

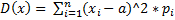, где а = М(Х). Или D(X) = M(X²)- (M(X))²

Свойства дисперсии случайной величины

1. Дисперсия постоянной величины есть нулю: D(C) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D (CX) = C²D(X)

3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий

13 Геометрическое распределение, параметры распределения

Со схемой испытаний Бернулли можно связать еще одну случайную величину  - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + 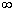и ее распределение определяется формулой

p_k = P ( = k) = q^k- 1 p, 0 < p <1, k =1, 2, …, , , .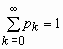

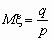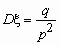Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 - p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k - 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k - 1 неудач, а в k-ое испытание — удача, равна 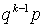. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность 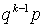. Этот закон распределения и называется геометрическим распределением . Название происходит из того, что величина 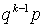представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать: 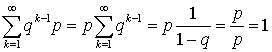, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем: 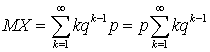. Для вычисления суммы воспользуемся следующим приемом — заменим 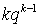на 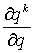и вынесем производную за знак суммы, в итоге получим: 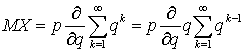. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна 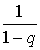. Вычисляя производную, запишем: 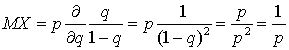. Аналогично можно получить выражение для 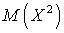: 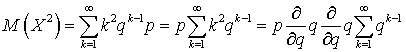. Заменяя сумму на ее значение 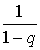, вычисляем: 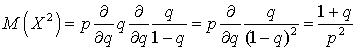. Таким образом, имеем выражение для дисперсии: 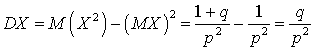. Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).