Метод градиента

Метод градиента в чистом виде формирует шаг по переменным как функцию от градиента R(x) в текущей точке поиска. Простейший алгоритм поиска min R(x) записывается в векторной форме следующим образом:

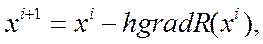
или в скалярном виде:

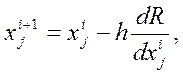
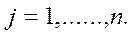- порядковый номер аргумента,

Величина рабочего шага в направлении градиента h grad R(x) зависит от величины градиента, который заранее учесть трудно, и от коэффициента пропорциональности шага h, с помощью которого можно управлять эффективностью метода.

Поиск каждой новой точки состоит из двух этапов:

1) оценка градиента R(x) путем вычисления частных производных от R(x) по каждой переменной х_j,

2) рабочий шаг по всем переменным одновременно.

Величина h сильно влияет на эффективность метода. Большей эффективностью обладает вариант метода, когда шаг по переменной определяется направляющими косинусами градиента.

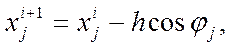
где cosφ _j =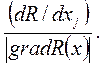

В этом случае величина рабочего шага не зависит от величи­ны модуля градиента, и ею легче управлять изменением h. В рай­оне оптимума может возникать значительное "рыскание", поэто­му используют различные алгоритмы коррекции h.

Наибольшее распространение получили следующие алго­ритмы:

MathCAD

1. hⁱ = const = h (без коррекции);

2. hⁱ = h^i-1 /2, если R(xⁱ) < R(x^i-1); hⁱ = h^i-1, R(xⁱ) > R(x^i-1);

3. hⁱ = h^i-1, если a₁≤ a ≤a₂; hⁱ =2 h^i-1, еслиa₁>a; 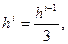если a₂ < a.

где a — угол между градиентами на предыдущем и текущем ша­ге; a₁ и a₂ — заданные пороговые значения выбираются субъек­тивно (например, a₁ = π/6, a₂ = π/3).

Вдали от оптимума направление градиента меняется мало, по­тому шаг можно увеличить (второе выражение), вблизи от опти­мума направление резко меняется (угол между градиентами R(x) большой), поэтому h сокращается (третье выражение).

Для оценки частных производных используются разностные методы:

1. Алгоритм с центральной пробой

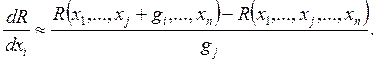
2. Алгоритм с парными пробами

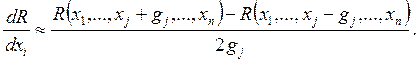
где g_j — пробный шаг по j -й переменной, выбираемый достаточ­но малым для разностной оценки производной.

Первый алгоритм требует меньших затрат по сравнению со вторым (обычно затраты выражаются количеством вычислений критерия оптимальности), но позволяет получить решение менее точно, чем второй, и эта погрешность зависит от величины проб­ного шага.

На рис. приведена одна из возможных траекторий поиска минимума двумерной функции градиентным методом (наряду с другими ниже рассматриваемыми методами).

Условием окончания поиска может являться малость модуля градиента R(x), т.е. | grad R(x) | <e.

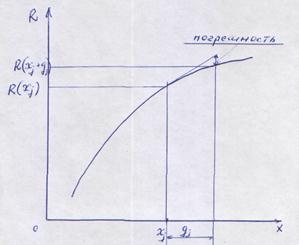
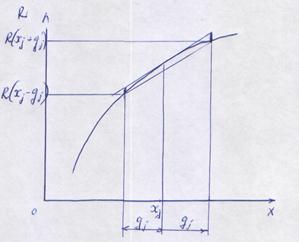
Рис. Иллюстрация получения производной с центральной и парными пробами.