1. Команда (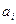 ,
, 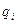 )
) 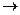 (
(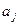 , Л,
, Л, 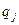 ) определяет переход Машины Тьюринга из состояния … в состояние …
) определяет переход Машины Тьюринга из состояния … в состояние …
2. Команда (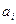 ,
, 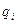 )
) 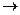 (
(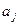 , Л,
, Л, 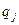 ) определяет следующую замену символов на ленте Машины Тьюринга…
) определяет следующую замену символов на ленте Машины Тьюринга…
3. Система команд: 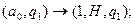
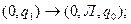
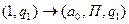 определяет следующую программу машины Тьюринга…
определяет следующую программу машины Тьюринга…
4. Машина Тьюринга задана системой команд: 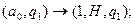
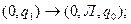
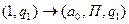 .
.
После двух тактов ее работы слово 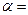

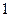
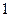
 переработается в слово
переработается в слово 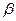 :
:
A) 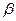 =
=  00
00  ; B)
; B) 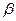 =
= 
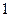
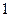
 ; C)
; C) 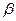 =
= 


 ;
;
D) 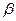 =
= 
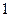

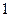 ; E)
; E) 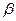 =0
=0 
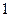
 .
.
5. Машина Тьюринга задана своей программой:

| |||
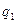
| 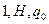
| 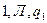
| 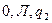
|
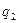
| 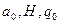
| 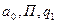
| 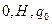
|
После двух тактов ее работы слово 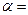

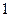
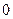
 переработается в слово
переработается в слово 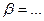
6. Машина Тьюринга задана своей программой:

| |||
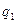
| 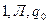
| 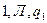
| 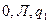
|
После трех тактов ее работы слово 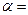

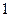
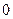
 переработается в слово
переработается в слово 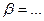
7. Нуль-функция (в двоичной системе счисления) реализуется с помощью Машины Тьюринга, заданной следующей программой:
| A) | 
| |||
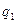
| 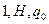
| 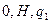
| 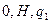
|
| B) | 
| |||
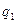
| 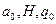
| 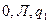
| 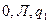
|
| C) | 
| |||
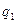
| 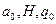
| 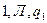
| 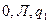
|
| D) | 
| |||
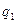
| 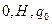
| 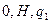
| 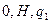
|
| E) | 
| |||
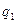
| 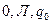
| 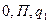
| 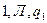
|
8. Функция 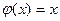 (в двоичной системе счисления) реализуется с помощью машины Тьюринга, заданной следующей программой…
(в двоичной системе счисления) реализуется с помощью машины Тьюринга, заданной следующей программой…
9. Функция следования 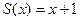 (в двоичной системе счисления) реализуется с помощью машины Тьюринга, заданной программой…
(в двоичной системе счисления) реализуется с помощью машины Тьюринга, заданной программой…
10. Простейшей является следующая функция:
A) 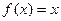 ; B)
; B) 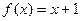 ; C)
; C) 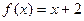 ;
;
D) 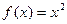 ; E)
; E) 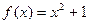 .
.
11. Простейшей является следующая функция:
A) 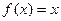 ; B)
; B) 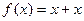 ; C)
; C) 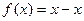 ;
;
D) 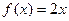 ; E)
; E) 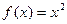 .
.
12. Значение функции проектора 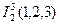 равно…
равно…
13. Значение функции 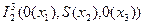 при
при 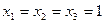 равно…
равно…
14. Суперпозицией функций 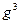 и
и 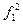 ,
, 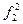 ,
, 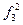 является k-местная функция при
является k-местная функция при 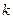 равном…
равном…
15. Суперпозицией функций 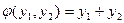 ,
, 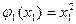 и
и 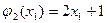 является следующая функция:
является следующая функция:
A) 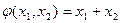 ; B)
; B) 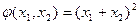 ;
;
C) 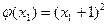 ; D)
; D) 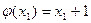 ; E)
; E) 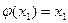 .
.
16. Суперпозицией функций 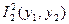 и
и 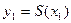 ,
, 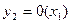 является следующая функция…
является следующая функция…
17. Суперпозицией функций 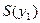 и
и 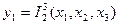 является функция…
является функция…
18. В результате работы оператора минимизации из k-местной функции получается m-местная функция для:
A) 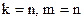 ; B)
; B) 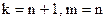 ; C)
; C) 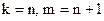 ;
;
D) 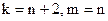 ; E)
; E) 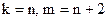 .
.
19. В результате работы оператора примитивной рекурсии из k и m местных функций получается l-местная функция для:
A) 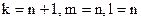 ; B)
; B) 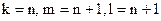 ;
;
C) 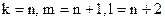 ; D)
; D) 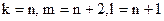 ;
;
E) 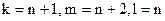 .
.
20. Если заданы функции 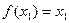 и
и 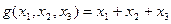 , и
, и 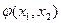 получена из данных с помощью оператора примитивной рекурсии, то
получена из данных с помощью оператора примитивной рекурсии, то 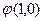 равно…
равно…
21. Если заданы функции 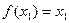 и
и 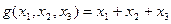 , и
, и 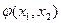 получена из данных с помощью оператора примитивной рекурсии, то
получена из данных с помощью оператора примитивной рекурсии, то 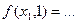
22. Если заданы функции 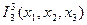 и S(x), и
и S(x), и 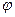 получена из данных с помощью оператора примитивной рекурсии, то
получена из данных с помощью оператора примитивной рекурсии, то 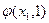 равно:
равно:
A) 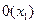 ; B)
; B) 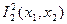 ; C)
; C) 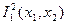 ; D)
; D) 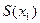 ;
;
E) 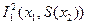 .
.
23. Если задана 3-местная функция 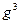 и
и 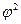 - 2-местная функция полученная из
- 2-местная функция полученная из 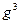 с помощью оператора минимизации, то
с помощью оператора минимизации, то 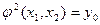 тогда и только тогда, когда:
тогда и только тогда, когда:
A) 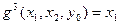 ; B)
; B) 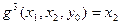 ;
;
C) 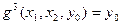 ; D)
; D) 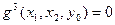 ;
;
E) 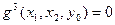 , где
, где 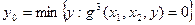 .
.
24. Если 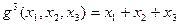 и
и 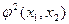 получена из
получена из 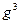 с помощью оператора минимизации, то
с помощью оператора минимизации, то 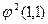 равно…
равно…
25. Если 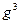 =
= 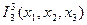 и
и 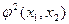 получена из
получена из 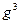 с помощью оператора минимизации, то
с помощью оператора минимизации, то 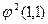 равно…
равно…
26. Алгоритмически разрешимой является следующая проблема:
A) непротиворечивости формул алгебры высказываний;
B) непротиворечивости формул алгебры предикатов;
C) 10-ая проблема Гильберта;
D) остановки машины Тьюринга;
E) распознавания «тождества» слов в группе.
27. Алгоритмически неразрешимой является следующая проблема:
A) непротиворечивости исчисления высказываний;
B) непротиворечивости исчисления предикатов;
C) разрешимости квадратных уравнений в поле действительных чисел;
D) разрешимости линейных уравнений в поле действительных чисел;
E) разрешимости системы линейных уравнений в поле действительных чисел.
28. Функция называется примитивно-рекурсивной, если она может быть получена из…
29. Верно следующее утверждение:
A) примитивно-рекурсивная функция не является общерекурсивной;
B) примитивно-рекурсивная функция не является частично-рекурсивной;
C) общерекурсивная функция является примитивно-рекурсивной;
D) общерекурсивная функция является частично-рекурсивной;
E) частично-рекурсивная функция является общерекурсивной.
30. Функция 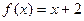 является
является
A) частично-рекурсивной, но не примитивно-рекурсивной;
B) примитивно-рекурсивной;
C) примитивно-рекурсивной, но не общерекурсивной;
D) не общерекурсивной;
E) не частично-рекурсивной.
31. Всякая простейшая функция:
A) не является общерекурсивной;
B) не является частично-рекурсивной;
C) является общерекурсивной, но не частично-рекурсивной;
D) является примитивно-рекурсивной и частично-рекурсивной;
E) является общерекурсивной, но не примитивно-рекурсивной.
32. Из тезиса Чёрча-Тьюрнга следует, что класс функций, вычислимых на машине Тьюринга совпадает с классом функций:
A) примитивно-рекурсивных;
B) частично-рекурсивных;
C) общерекурсивных;
D) частично-рекурсивных, но не общерекурсивных;
E) общерекурсивных, но не примитивно-рекурсивных.
 2015-01-30
2015-01-30 321
321








