1. Число видов символов исчисления высказываний равно…
2. Число групп аксиом исчисления высказываний равно…
3. Аксиомой исчисления высказываний является следующая формула:
A) 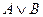 ; B)
; B) 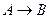 ; C)
; C) 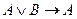 ;
;
D) 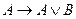 ; E)
; E) 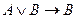 .
.
4. Аксиомой исчисления высказываний является следующая формула:;
A) 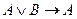 ; B)
; B) 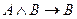 ; C)
; C) 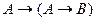 ;
;
D) 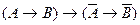 ; E)
; E) 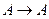 .
.
5. Теория Т` называется эффективно аксиоматизируемой если…
6. Последовательность формул 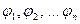 называется выводом теоремы
называется выводом теоремы 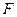 этой теории, если…
этой теории, если…
7. Следующая последовательность формул является доказательством:
A) 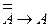 ,
, 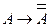 ,
, 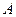 ;
;
B) 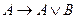 ,
, 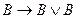 ,
, 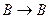 ;
;
C) 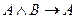 ,
, 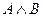 ,
, 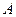 ;
;
D) 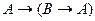 ,
, 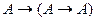 ;
;
E) 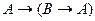 ,
, 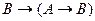 .
.
8. Формула Q теории Т называется теоремой теории Т, если…
9. Формула 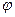 исчисления высказываний является теоремой тогда и только тогда, когда в алгебре высказываний:
исчисления высказываний является теоремой тогда и только тогда, когда в алгебре высказываний:
A) 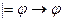 ; B)
; B) 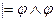 ; C)
; C) 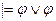 ;
;
D) 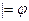 ; E)
; E) 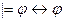 .
.
10. Теория Т называется разрешимой, если…
11. Основными правилами вывода исчисления высказываний являются правила…
12. Если 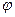 аксиома исчисления высказываний, то:
аксиома исчисления высказываний, то:
A) 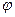 не является теоремой исчисления высказываний;
не является теоремой исчисления высказываний;
B) 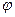 не является выполнимой формулой алгебры высказываний;
не является выполнимой формулой алгебры высказываний;
C) 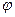 - тождественно-ложная формула алгебры высказываний;
- тождественно-ложная формула алгебры высказываний;
D) 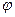 - тавтология алгебры высказываний;
- тавтология алгебры высказываний;
E) 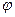 теорема с минимальной длиной доказательства 2.
теорема с минимальной длиной доказательства 2.
13. Если Г некоторое множество формул теории Т и 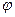 некоторая формула этой теории, то
некоторая формула этой теории, то
A) из 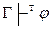 следует
следует 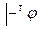 ;
;
B) из 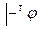 следует
следует 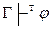 ;
;
C) из 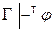 следует
следует 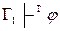 , где
, где 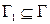 ;
;
D) из 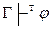 следует
следует 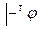 если
если 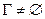 ;
;
E) из 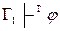 следует
следует 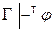 , если
, если 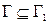 .
.
14. Если Г некоторое множество формул теории Т и 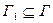 и
и 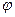 некоторая формула этой теории, то:
некоторая формула этой теории, то:
A) из 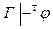 следует
следует 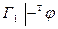 ;
;
B) из 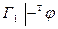 следует
следует 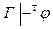 ;
;
C) из 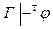 и
и 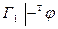 следует
следует 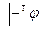 ;
;
D) 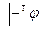 ; E) из
; E) из 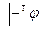 не следует, что
не следует, что 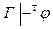 .
.
15. Запись теоремы дедукции имеет вид…
16. Запись обобщенной теоремы дедукции имеет вид…
17. Запись теоремы обратной к теореме дедукции имеет вид…
18. Если Г= 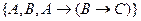 и из
и из 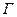

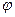 , то по обобщенной теореме дедукции:
, то по обобщенной теореме дедукции:
A) 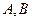

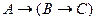 ; B)
; B) 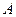

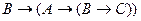 ;
;
C) 
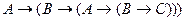 ;
;
D) 
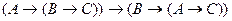 ;
;
E) 
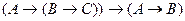 .
.
19. Если 
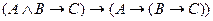 , то по теореме обратной к обобщенной теореме дедукции:
, то по теореме обратной к обобщенной теореме дедукции:
A) 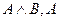

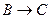 ; B)
; B) 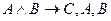

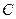 ;
;
C) 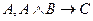

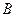 ; D)
; D) 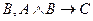

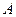 ;
;
E) 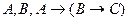

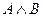 .
.
20. Если 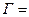
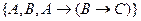 и
и 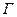

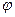 , то по теореме дедукции:
, то по теореме дедукции:
A) 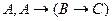

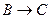 ; B)
; B) 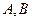

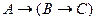 ;
;
B) C) 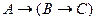

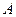 ; D)
; D) 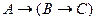

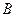 ;
;
E) 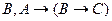

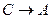 .
.
21. Если  Г=
Г= 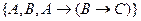 и из
и из 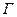

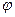 , то:
, то:
A) 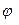 =
= 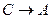 ; B)
; B) 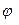 =
= 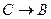 ; C)
; C) 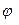 =
= 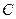 ;
;
D) 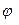 =
= 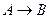 ; E)
; E) 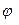 =
= 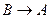 ;
;
22. Символическая запись правила силлогизма исчисления высказываний имеет вид…
23. Символическая запись правила соединения посылок исчисления высказываний имеет вид…
24. Символическая запись правила доказательства разбором случаев имеет вид:
A) 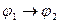 ├
├ 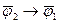 ;
;
B) 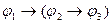 ├
├ 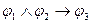 ;
;
C) 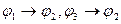 ├
├ 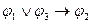 ;
;
D) 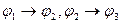 ├
├ 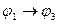 ;
;
E) 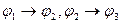 ├
├ 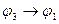 .
.
25. Применение правила заключения к формулам 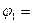
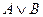 и
и 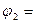
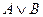
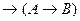 дает следующую формулу
дает следующую формулу 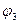 :
:
A) 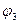 =
= 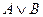 ; B)
; B) 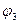 =
= 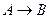 ; C)
; C) 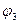 =
= 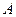 ;
;
D) 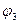 =
= 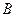 ; E)
; E) 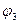 =
= 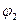 .
.
26. Применение правила заключения к формулам 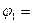
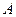 и
и 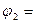
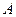
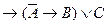 дает следующую формулу
дает следующую формулу 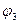 …
…
27. Если 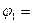
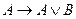 ,
, 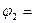
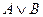
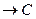 , то по правилу силлогизма получается следующая формула
, то по правилу силлогизма получается следующая формула 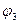 …
…
28. Если 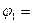
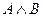 ,
, 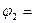
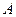 ,
, 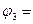
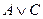 , то по правилу перестановки посылок исчисления высказываний:
, то по правилу перестановки посылок исчисления высказываний:
A) 
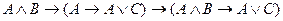 ;
;
B) 
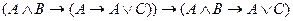 ;
;
C) 
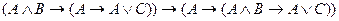 ;
;
D) 
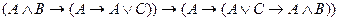 ;
;
E) 
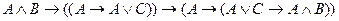 .
.
29. Если 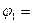
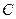 ,
, 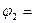
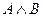 ,
, 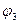 =
= 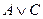 , то по правилу соединения посылок исчисления высказываний:
, то по правилу соединения посылок исчисления высказываний:
A) 
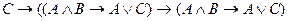 ;
;
B) 
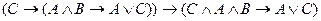 ;
;
C) 
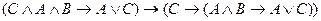 ;
;
D) 
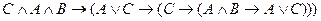 ;
;
E) 
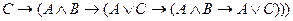 .
.
30. Если 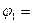
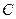 ,
, 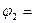
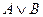 , то по правилу контрапозиции исчисления высказываний:
, то по правилу контрапозиции исчисления высказываний:
A) 
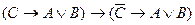 ;
;
B) 
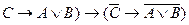 ;
;
C) 
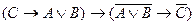 ;
;
D) 
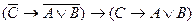 ;
;
E) 
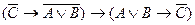 .
.
31. Если 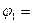
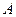 ,
, 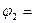
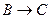 , то по правилу удаления конъюнкции исчисления высказываний:
, то по правилу удаления конъюнкции исчисления высказываний:
A) 
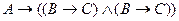 ;
;
B) 
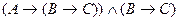 ;
;
C) 
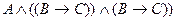 ;
;
D) 
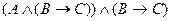 ;
;
E) 
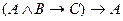 .
.
32. Если 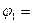
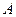 ,
, 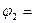
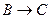 , то по правилу удаления дизъюнкции исчисления высказываний:
, то по правилу удаления дизъюнкции исчисления высказываний:
A) 
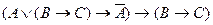 ;
;
B) 
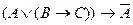 ;
;
C) 
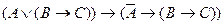 ;
;
D) 
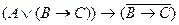 ;
;
E) 
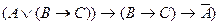 .
.
33. Исчисление высказываний является:
A) полной и пополнимой теорией (полной в узком смысле);
B) полной, но не пополнимой;
C) не полной, и не пополнимой;
D) не полной, нo пополнимой;
E) нельзя выяснить.
34. Исчисление высказываний является:
A) не полной теорией;
B) не пополнимой теорией;
C) не разрешимой теорией;
D) зависимой теорией;
E) противоречивой теорией.
35. Формула 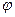 исчисления высказываний называется эквивалентной формуле
исчисления высказываний называется эквивалентной формуле 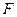 исчисления высказываний если:
исчисления высказываний если:
A) ├ 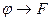 ; B) ├
; B) ├ 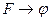 ; C) ├
; C) ├ 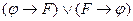 ;
;
D) ├ 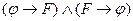 ; E) ├
; E) ├ 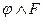 .
.
36. Для доказательства эквивалентности 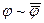 достаточно доказать:
достаточно доказать:
A) ├ 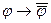 ; B) ├
; B) ├ 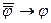 ; C) ├
; C) ├ 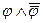 ;
;
D) ├ 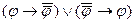 ; E) ├
; E) ├ 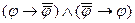 .
.
37. Для доказательства симметричности отношения эквивалентности (т.е. из 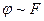 следует
следует 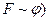 достаточно доказать, что:
достаточно доказать, что:
A) Из ├ 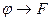 следует ├
следует ├ 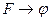 ;
;
B) Из ├ 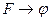 следует ├
следует ├ 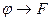 ;
;
C) Из ├ 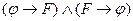 следует ├
следует ├ 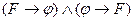 ;
;
D) Из ├ 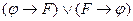 следует ├
следует ├ 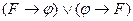 ;
;
E) Из ├ 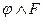 следует ├
следует ├ 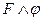 .
.
38. Для доказательства транзитивности отношения эквивалентности формул исчисления высказываний достаточно доказать, что:
A) 
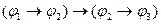 ;
;
B) 
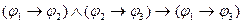 ;
;
C) из 
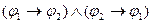 и
и 
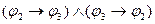 следует
следует 
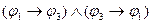 ;
;
D) из 
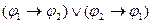 и
и 
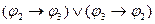 следует
следует 
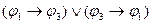 ;
;
E) из 
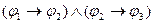 следует
следует 
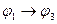 ;
;
39. В исчислении высказываний 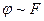 (формуле
(формуле 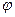 эквивалента формуле
эквивалента формуле 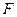 ) тогда и только тогда когда в алгебре высказываний…
) тогда и только тогда когда в алгебре высказываний…
40. Формальная теория Т (содержащая знак отрицания) называется непротиворечивой, если для любой ее формулы 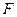 …
…
41. Непротиворечивая формальная теория Т содержащая знак отрицания называется полной, если для любой ее формулы 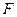 …
…
42. Аксиома 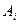 называется независимой относительно системы аксиом
называется независимой относительно системы аксиом 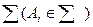 формальной теории Т если:
формальной теории Т если:
43. Для доказательства независимости аксиомы 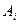 относительно непротиворечивой системы аксиом
относительно непротиворечивой системы аксиом 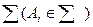 достаточно доказать, что…
достаточно доказать, что…
44. Теоремой исчисления высказываний является следующая формула 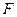 исчисления высказываний:
исчисления высказываний:
A) 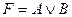 ; B)
; B) 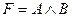 ; C)
; C) 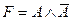 ;
;
D) 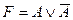 ; E)
; E) 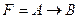 .
.
45. Теоремой исчисления высказываний является следующая формула:
A) 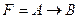 ; B)
; B) 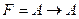 ; C)
; C) 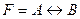 ;
;
D) 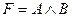 ; E)
; E) 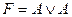 .
.
46. Теоремой исчисления высказываний является следующая формула исчисления высказываний:
A) 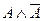 ; B)
; B) 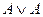 ; C)
; C) 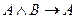 ; D)
; D) 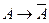 ; E)
; E) 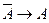 .
.
47. Формула 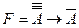 исчисления высказываний является теоремой исчисления высказываний с минимальной длиной доказательства n равной…
исчисления высказываний является теоремой исчисления высказываний с минимальной длиной доказательства n равной…
48. Формула 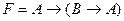 является теоремой исчисления высказываний с минимальной длиной доказательства n равной…
является теоремой исчисления высказываний с минимальной длиной доказательства n равной…
49. Теорема исчисления высказываний 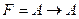 может быть получена применением правила силлогизма из следующих аксиом
может быть получена применением правила силлогизма из следующих аксиом 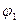 и
и 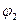 :
:
A) 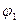 =
= 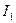 ,
, 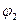 =
= 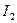 ; B)
; B) 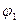 =
= 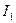 ,
, 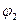 =
= 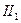 ;
;
C) 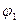 =
= 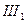 ,
, 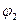 =
= 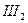 ; D)
; D) 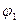 =
= 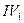 ,
, 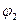 =
= 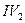 ;
;
E) 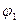 =
= 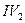 ,
, 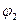 =
= 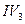 .
.
50. Исчисление высказываний является:
A) неполной теорией;
B) не пополнимой теорией;
C) зависимой теорией;
D) разрешимой теорией;
E) противоречивой теорией.
51. Для доказательства рефлексивности отношения эквивалентности формул исчисления высказываний достаточно доказать, что…
52. Для доказательства эквивалентности 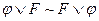 достаточно доказать, что…
достаточно доказать, что…
53. Теоремой исчисления высказываний является следующая формула:
A) 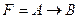 ; B)
; B) 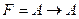 ; C)
; C) 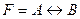 ;
;
D) 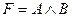 ; E)
; E) 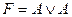 .
.
54. В результате подстановки 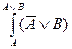 получается формула эквивалентная следующей формуле исчисления высказываний…
получается формула эквивалентная следующей формуле исчисления высказываний…
55. В результате подстановки 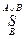 (
(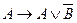 ) получается следующая формула исчисления высказываний…
) получается следующая формула исчисления высказываний…
56. В результате подстановки 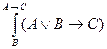 получается следующая формула исчисления высказываний…
получается следующая формула исчисления высказываний…
 2015-01-30
2015-01-30 763
763








