1. Следующее «слово» является формулой исчисления предикатов:
A) 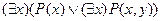 ; B)
; B) 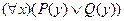 ;
;
C) 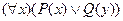 ; D)
; D) 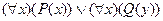 ;
;
E) 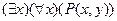 .
.
2. Следующее «слово» является формулой исчисления предикатов:
A) 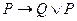 ; B)
; B) 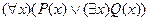 ;
;
C) 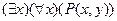 ; D)
; D) 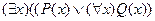 ;
;
E) 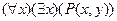 .
.
3. Следующая формула является аксиомой исчисления предикатов:
A) 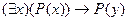 ; B)
; B) 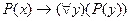 ;
;
C) 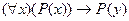 ; D)
; D) 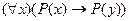 ;
;
E) 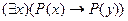 .
.
4. Следующая формула является аксиомой исчисления предикатов:
A) 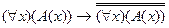 ; B)
; B) 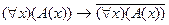 ;
;
C) 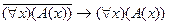 ; D)
; D) 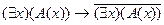 ;
;
E) 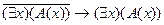 .
.
5. Следующая формула является аксиомой исчисления предикатов:
A) 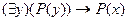 ; B)
; B) 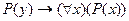 ;
;
C) 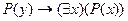 ; D)
; D) 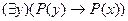 ;
;
E) 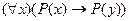 .
.
6. Основным правилом вывода исчисления предикатов является правило:
A) cиллогизма; B) перестановки посылок;
C) введение квантора существования;
D) удаление квантора существования;
E) удаление квантора общности.
7. Правило введения квантора общности исчисления предикатов имеет вид:
A) 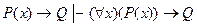 ;
;
B) 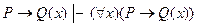 ;
;
C) 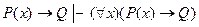 ;
;
D) 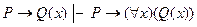 ;
;
E) 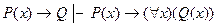 .
.
8. Правило введения квантора существования исчисления предикатов имеет вид…
9. Формула F исчисления предикатов является теоремой тогда и только тогда, когда в алгебре предикатов она является…
10. Следующая формула является теоремой исчисления предикатов:
A) 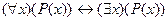 ; B)
; B) 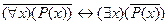 ;
;
C) 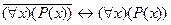 ; D)
; D) 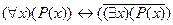 ;
;
E) 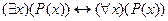 .
.
11. Следующая формула является теоремой исчисления предикатов:
A) 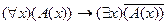 ; B)
; B) 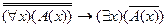 ;
;
C) 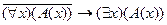 ; D)
; D) 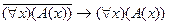 ;
;
E) 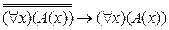 .
.
12. Следующая формула является аксиомой исчисления предикатов с равенством:
A) 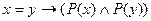 ; B)
; B) 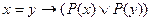 ;
;
C) 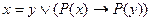 ; D)
; D) 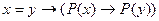 ;
;
E) 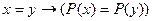 .
.
13. Следующая формула является теоремой исчисления предикатов с равенством:
A) 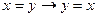 ; B)
; B) 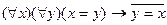 ;
;
C) 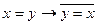 ; D)
; D) 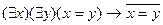 ;
;
E) 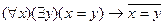 .
.
14. Следующая формула является аксиомой формальной арифметики:
A) 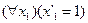 ; B)
; B) 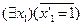 ; C)
; C) 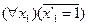 ;
;
D) 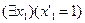 ; E)
; E) 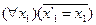 .
.
15. Следующая формула является аксиомой формальной арифметики:
A) 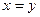 ; B)
; B) 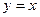 ; C)
; C) 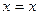 ; D)
; D) 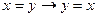 ;
;
E) 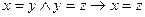 .
.
16. Исчисление предикатов является теорией:
A) полной; B) не пополнимой; C) полной в узком смысле; D) пополнимой; E) не полной, и не пополнимой.
17. Исчисление предикатов с равенством является:
A) узким исчислением предикатов;
B) исчислением предикатов 1-го порядка;
C) теорией со стандартной формализацией;
D) исчислением предикатов 2-го порядка;
E) теорией 2-го порядка.
18. Формальная арифметика является:
A) исчислением предикатов 1-го порядка;
B) теорией 2-го порядка;
C) теорией со стандартной формализацией;
D) частью исчисления предикатов;
E) частью исчисления предикатов с равенством.
19. Следующее предложение является первой теоремой Гёделя. Если T- формальная арифметика, то эта теория:
A) непротиворечива; B) независима;
C) разрешимая; D) не полная, но пополнимая;
E) не полная и не пополнимая.
20. Следующее предложение является второй теоремой Гёделя. Если T- формальная арифметика и F- формула, в которой утверждается непротиворечивость T, то:
A) F- зависима относительно T; B) F и 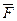 недоказуемы в T;
недоказуемы в T;
C) F доказуема в T; D) F или 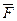 доказуемы в T;
доказуемы в T;
E) 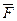 - зависима относительно T.
- зависима относительно T.
21. Разрешимой является следующая теория (исчисление):
A) высказываний; B) предикатов;
C) предикатов с равенством; D) формальная арифметика;
E) формальная теория групп.
 2015-01-30
2015-01-30 444
444








