Лекция 6. Проверка общего качества уравнения парной линейной регрессии: построение таблицы дисперсионного анализа

Проверка общего качества уравнения парной линейной регрессии: построение таблицы дисперсионного анализа, вычисление коэффициента детерминации и проверка его значимости, стандартная ошибка уравнения регрессии. Оценка значимости коэффициентов уравнения парной линейной регрессии, построение доверительных интервалов для коэффициентов

Доверительный интервал для прямой регрессии. Прогнозирование в парных регрессионных моделях. Ошибка прогноза. Доверительный интервал прогноза. Условия Гаусса-Маркова. Теорема Гаусса-Маркова

Парная регрессия представляет собой уравнение, описывающее связь между двумя переменными: зависимой переменной 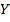и независимой переменной 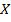. Иногда переменную 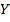называют результатом, а переменную 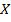– фактором: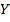 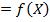, при этом функция может быть как линейной, так и нелинейной. В данной главе более детально рассмотрим линейную парную регрессию. Предположим, что у нас есть набор значений двух переменных 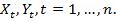Соответствующие пары 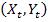можно изобразить на одной плоскости:

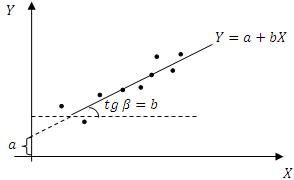
Параметр 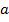соответствует отрезку прямой, отсекаемому линией регрессии при пересечении с осью ординат, параметр b определяет наклон линии регрессии к оси абсцисс. При этом параметр a традиционно принято называть свободным членом регрессии, а параметр 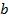– коэффициентом регрессии, который показывает, на сколько единиц в среднем изменится значение 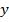при изменении 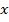на одну единицу.

Допустим, что нашей задачей является подбор функции 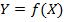из параметрического семейства функций 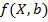наилучшим образом описывающая зависимость 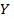от 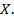В качестве меры отклонения функции 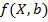от исходных наблюдений можно использовать:

- сумму квадратов отклонений;

- сумму модулей отклонений;

- другие меры отклонений.

Согласно методу наименьших квадратов (МНК) неизвестные параметры модели выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений от модельных была минимальной:

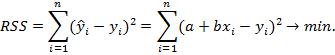
Среди преимуществ метода наименьших квадратов следует особенно отметить лёгкость вычислительной процедуры и хорошие по статистическим свойствам оценки. Данные факты объясняют широкое применение данного метода в статистическом анализе. Из недостатков наиболее существенным является – чувствительность к выбросам. Согласно необходимому условию экстремума функции нескольких переменных, необходимо найти частные производные по этим переменным и приравнять их к нулю. После ряда преобразований получим:

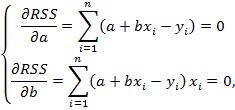
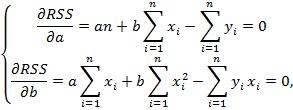
Разделим обе части полученной выше системы на 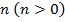, получим систему нормальных уравнений:

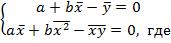
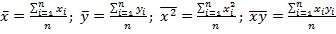
Решив полученную систему относительно неизвестных параметров 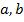, получим:

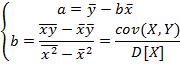
Таким образом, остатки, оцененные таким образом, можно представить следующим образом:

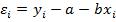
Свойства оценок МНК определяются предположениями относительно свойств случайного возмущения в модели наблюдений. Эти предположения обычно называются условиями Гаусса – Маркова.