Графическая интерпретация задачи оптимизации

С учетом соотношения 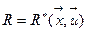(8) задачу оптимизации можно сформулировать: требуется найти вектор управления 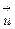такой, что при заданном векторе 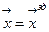критерий оптимальности R принял бы наилучшее значение. При этом управление 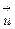связаны между собой в общем случае соотношениями 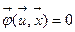(9), 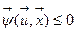(10), которые являются ограничениями в форме равенств (9) и неравенств (10) в задаче оптимизации. Часто эти ограничения являются критериями в многокритериальной задаче оптимизации, в которой 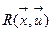- главный критерий, а и 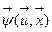переводятся в разряд ограничений.

Решение задачи оптимизации без учета ограничения (9), (10) называется решением задачи безусловной оптимизации с одним критерием R. С учетом (9), (10) задачи оптимизации будут называться задачами условной оптимизации. Используя выражения (8), (9), (10) постановку задачи оптимизации формально можно записать 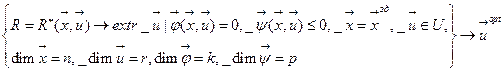(11)

Т.к. в задаче оптимизации 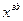(задание значение вектора) выступает как константа, то можно записать следующим образом: 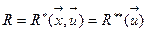, , 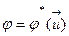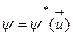(12).

Задачу (11) можно сформулировать и в след. виде 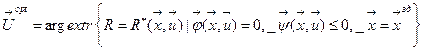(13)

В дальнейшем при изложении методов оптимизации с учетом соотношения (12) будем записывать , ,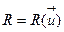

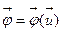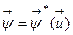
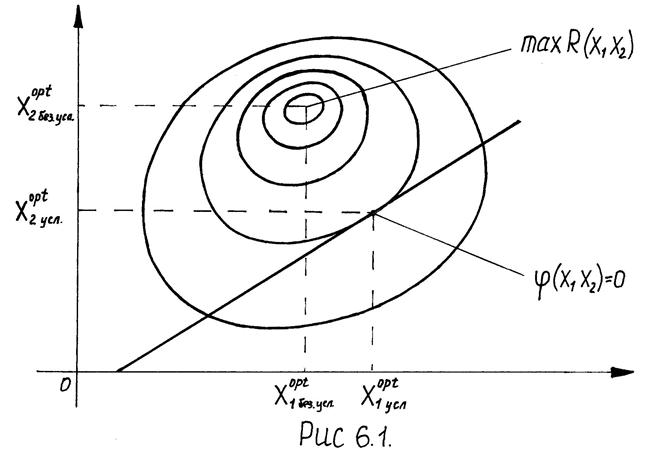
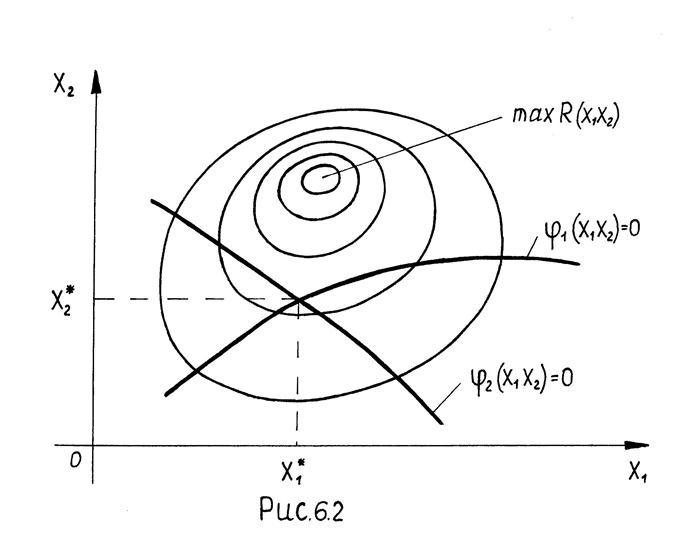
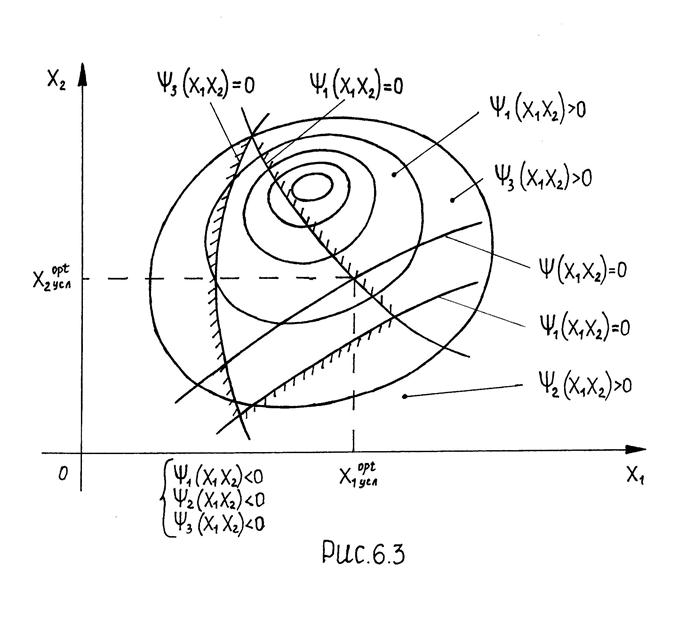
В соответствии с (13) графически задачу оптимизации можно интерпретировать следующим образом: рассмотрим задачу с 2-мя управлениями: рис 6. 1,2,3.

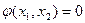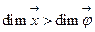Пусть R(x₁,x₂) имеет max. , то ; при 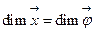задачи оптимизации нет (рис. 6.2).

Если размерность 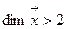, то для графической интерпретации отклика поверхности 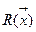берут 2 оси (координат) и через них проводят плоскость. Плоскостями, параллельными плоскости, проходящей через выбранные оси, рассекает плоскость 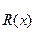(рис 6.3).

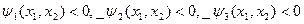. - любая.

Задача оптимизации в действующей технологии является определение оптимальных значений заданий регулятора технологических процессов.