Рассмотрим случай, когда в нашей задачи ограничения типа неравенств неактивны, т.е. точка экстремума лежит внутри области на 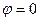 (Рис 26.1). Это означает, что правая часть соотношения
(Рис 26.1). Это означает, что правая часть соотношения
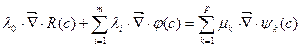 (4)
(4)
становится равной нулю, тогда
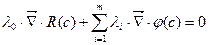 (5)
(5)
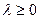 (6),
(6), 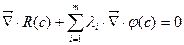 (7)
(7)
- условие Лагранжа, необходимое условие существования экстремума
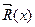 при наличии ограничений лишь типа равенств.
при наличии ограничений лишь типа равенств.
Условие Лагранжа получается как необходимое условие существования безусловного экстремума функции Лагранжа, имеющей вид
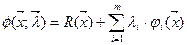 , (8)
, (8)
где 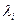 - неопределенные множители Лагранжа.
- неопределенные множители Лагранжа.
Условие (7) как необходимое условие существования условия (8).
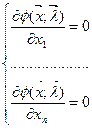
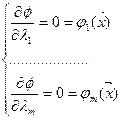
Т.о. необходимое условие существования безусловного экстремума 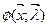 ее дифференцированием по переменным с приравниванием результата к
ее дифференцированием по переменным с приравниванием результата к
нулю и дополнением с системой уравнений ограничений типа равенств. Из решения находим 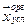 и
и 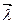
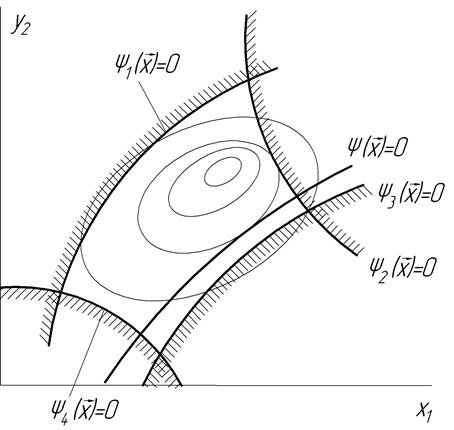
Рис. 26.1.
Распределение потоков сырья между параллельно работающим аппаратом.
Рассмотрим задачу распределения сырья в аппарате, неконкретизируя тип аппарата, вид критерия оптимальности. Считаем, что критерий оптимальности является суммой критериев оптимальности каждого аппарата, т.е. критерий аддитивен. (Рис. 26.2)
|
|
|
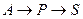
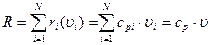 (1)
(1)
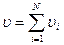 (2)
(2)
Условие (2) является ограничением в форме равенства в задаче распределения потоков.
Для решения используем метод неопределенных множителей Лагранжа.
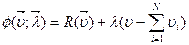 (3)
(3)
Ищем безусловный экстремум этой функции. Запишем систему необходимых условий существования функции Ф
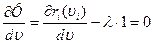
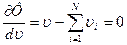 (4)
(4)
(3) и (4) необходимые условие сущ. экстр. 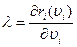
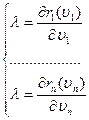 (5)
(5)
Для оптимального распределения потока сырья 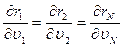 критерий оптимальности должен быть аддитивной функцией.
критерий оптимальности должен быть аддитивной функцией.
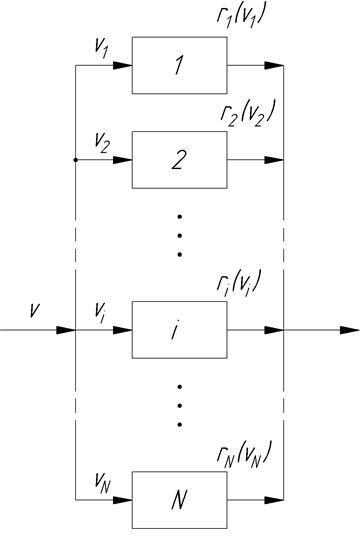
Рис. 26.2.
 2015-01-30
2015-01-30 460
460







