Разложим R(x) в окрестности точки, подозреваемой на экстремум
x0= col( 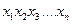 )
)
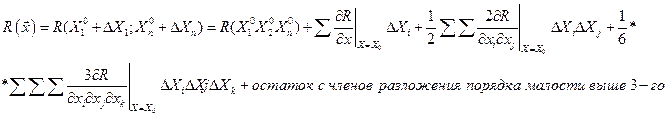
X0 удовлетворяет необходимым условиям существования R, тогда
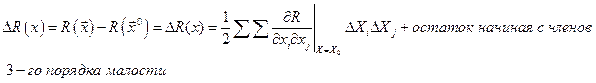 (3)
(3)
Из выражения (3) следует, то что, если пренебречь членами порядка малости выше 2-го знака приращения 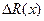 «±» определяется всеми производными 2-ого порядка, включая и смешанные. Частные производные вычисляются в т.
«±» определяется всеми производными 2-ого порядка, включая и смешанные. Частные производные вычисляются в т. 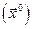 и их можно рассматривать как константы, поэтому необязательно требовать малости
и их можно рассматривать как константы, поэтому необязательно требовать малости 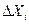
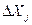 :
:
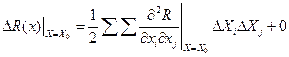 ,
,
обозначим 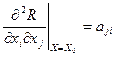
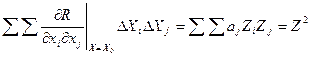
Если при любых 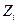 и
и 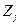 , кроме
, кроме  , Z2>0, а в точке 1 Z2=0, то Z2 положительно определена и в точке экстремума будет иметь минимум
, Z2>0, а в точке 1 Z2=0, то Z2 положительно определена и в точке экстремума будет иметь минимум  >0. Для положительной определенности квадратичной формы Z2 необходимо и достаточно чтобы все определители состояли из элементов
>0. Для положительной определенности квадратичной формы Z2 необходимо и достаточно чтобы все определители состояли из элементов 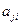 и были положительны.
и были положительны.
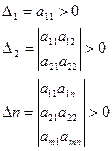 , тогда Х0 – доставляет min
, тогда Х0 – доставляет min 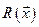 .
.
 2015-01-30
2015-01-30 266
266








