Рассмотрим случай, когда в нашей задачи ограничения типа неравенств
неактивны, т.е. точка экстремума лежит внутри области на 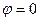 .
.
Это означает, что правая часть соотношения
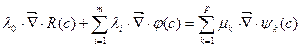 (4)
(4)
становится равной нулю, тогда
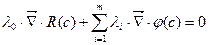 (5);
(5);
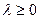 (6),
(6), 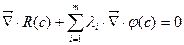 (7)
(7)
- условие Лагранжа, необходимое условие существования экстремума 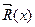 при наличии ограничений лишь типа равенств. Условие Лагранжа получается как необходимое условие существования безусловного экстремума функции Лагранжа, имеющей вид
при наличии ограничений лишь типа равенств. Условие Лагранжа получается как необходимое условие существования безусловного экстремума функции Лагранжа, имеющей вид
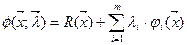 (8),
(8),
где 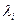 - неопределенные множители Лагранжа.
- неопределенные множители Лагранжа.
Условие (7) как необходимое условие существования экстремума (8).
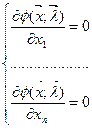
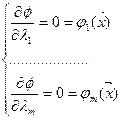
Т.о. необходимое условие существования безусловного экстремума 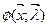 ее дифференцированием по переменным с приравниванием результата к нулю и дополнением с системой уравнений ограничений типа равенств. Из решения находим
ее дифференцированием по переменным с приравниванием результата к нулю и дополнением с системой уравнений ограничений типа равенств. Из решения находим 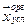 и
и 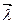 .
.
Рассмотрим пример:
Необходимо определить соотношение между высотой и диаметром цилиндрического аппарата имеющего крышку и дно («бочка»), объем которой задан, но изготовление, которой идет min количество материала, т.е. поверхность минимальна.
|
|
|
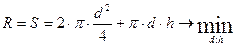
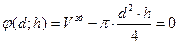

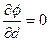 ;
; 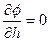 ;
; 


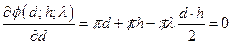




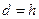
 2015-01-30
2015-01-30 549
549








