2014-10-30
1896
5. 
.
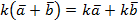6. 
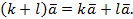
7. 
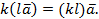
8. 
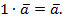
Упражнение. Даны векторы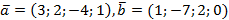 
. Найдите вектор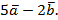 
Определение 5. Множество всех п – мерных арифметических векторов, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее восьми свойствам, называется арифметическим п – мерным векторным пространством и обозначается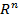 
.
Определение 6. Некоторое множество U образует линейное пространство, если для любых его элементов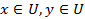 
определена операция сложения 
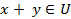и для каждого элемента 
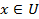и любого действительного числа 
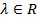определено произведение 
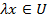причём эти операции удовлетворяют свойствам 1-8 (см. выше).
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа п.
Определение 7. Подмножество S линейного пространства U называется подпространством, если выполнены следующие два условия:
1. для любых двух векторов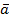 
и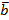 
из S их сумма 
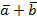также принадлежит S
2. для любого вектора 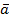из S и любого действительного числа 
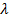произведение 
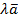также принадлежит S.
Очевидно, что подпространство S само является линейным пространством относительно операций сложения и умножения на число, определённых в U. У любого пространства существуют два подпространств, называемые тривиальными. Это само пространство U и нулевое подпространство (состоящее из одного нулевого элемента).
Например, в R3 (множество векторов) линейным подпространством будут все плоскости и все прямые, проходящие через начало координат.
Упражнение. Выяснить является ли множество S – множество решений неравенства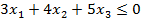 
линейным подпространством в R3.
Определение 8. Вектор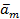 
называется линейной комбинацией векторов
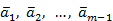, если
,
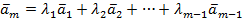где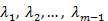 
- действительные числа.
Определение 9. Множество всех линейных комбинаций векторов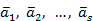 
называется линейной оболочкой векторов 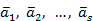и обозначается 
.
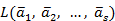Упражнение. Найти линейную оболочку векторов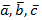 
и проверьте, принадлежит ли этой оболочке вектор 
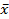, если 
.
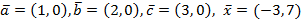3.2. Базис и размерность линейного пространства. Координаты вектора в данном базисе
Определение 10. Векторы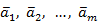 
называются линейно зависимыми, если существуют такие числа 
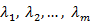, не равные одновременно нулю, что
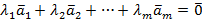. (1)
Если равенство выполняется только при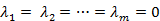 
, то векторы 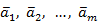называются линейно независимыми.
Пример. Система векторов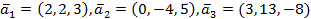 
линейно зависима, так как 
.
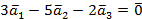Определение 11. Векторы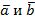 
называются коллинеарными, если они параллельны одной прямой, т.е. 
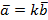или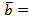 
.
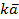Утверждение. Система, содержащая два вектора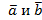 
, линейно зависима в том и только том случае, когда эти векторы коллинеарны.
Доказательство. Если оба вектора равны нулю, то они, очевидно, линейно зависимы и коллинеарны. Пусть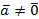 
. Допустим сначала, что векторы 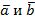линейно зависимы. Тогда 
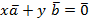для некоторых x и y, не равных нулю одновременно. Если 
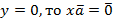. Но тогда и 
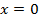, т.к. 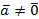. Если же 
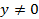, то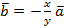 
. Предположим теперь, что векторы коллинеарны, т.е. 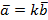. Т.к. их линейная комбинация 
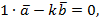то векторы 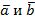линейно зависимы.
Определение 12. Три вектора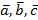 
в R3, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.
Упражнение. Доказать, что три вектора в R3 линейно зависимы в том и только том случае, когда они компланарны.
