В соответствии с этим методом приближенное решение задачи Коши ищется с помощью неявной разностной схемы

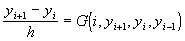
где 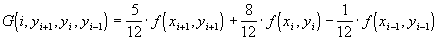. Значение 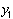определяется с помощью метода Рунге-Кутты. Для решения неявного нелинейного уравнения предлагается воспользоваться методом последовательных приближений:

.

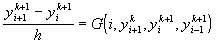В качестве нулевого приближения 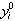можно использовать решение, полученное с помощью явной двухшаговой схемы Адамса.

Рассмотрим этот процесс на нашем примере. Будем использовать обозначения:

, , .

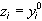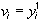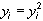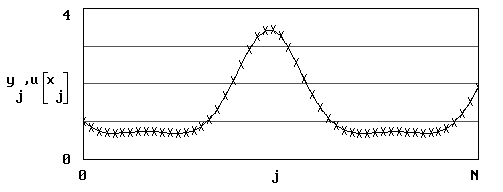
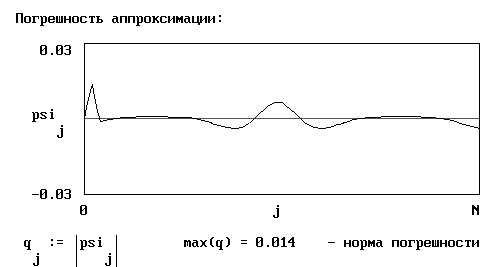
Тогда, используя средства пакета MathCAD, получим:

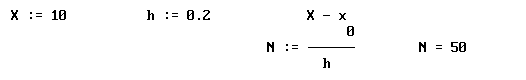
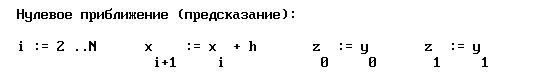
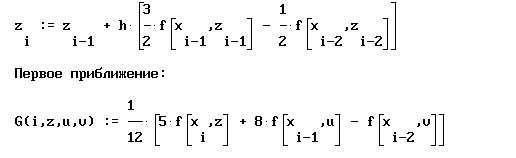
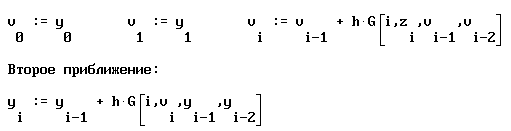
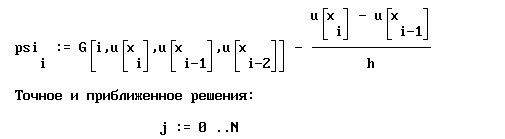
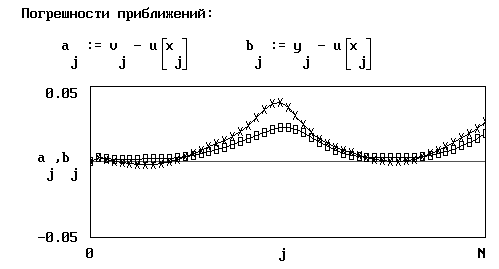
Численное решение двухточечной краевой задачи для обыкновенного дифференциального уравнения второго порядка.

Тема. Численное решение краевой задачи для линейного дифференциального уравнения второго порядка в самосопряженной форме с краевыми условиями первого рода. Применение разностной схемы второго порядка аппроксимации.

Пример. Дана краевая задача:

, , .

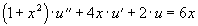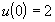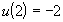Методами теории дифференциальных уравнений можно найти общее решение этого линейного неоднородного уравнения:

.

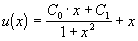Умножив дифференциальное уравнение на функцию 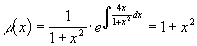, приведем его к самосопряженному виду:

,

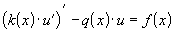где 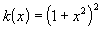, , 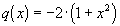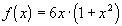. Тогда разностная схем второго порядка аппроксимации будет иметь вид:

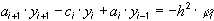
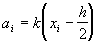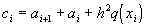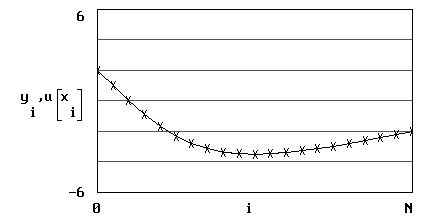
где , , 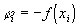. Для решения этой системы линейных уравнений можно применить метод прогонки.

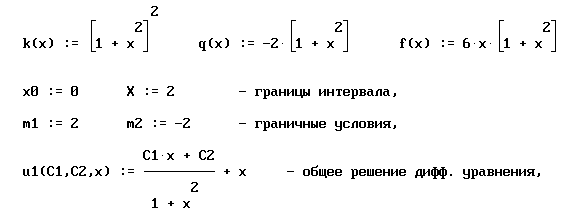
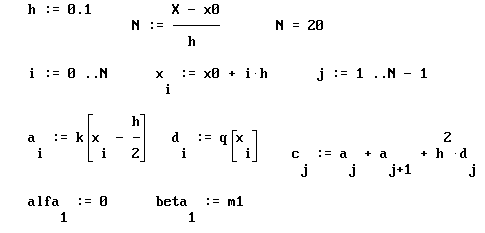
[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]

[Home|Кафедра|ПетрГУ]

[Home|Кафедра|ПетрГУ]