1-10. Найти области определения данных функций
1. а) 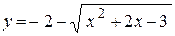 ; ;
| б) 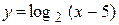 . .
|
2. а) 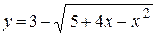 ; ;
| б) 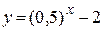 . .
|
3. а) 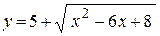 ; ;
| б) 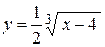 . .
|
4. а) 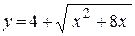 ; ;
| б) 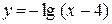 . .
|
5. а) 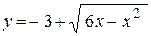 ; ;
| б) 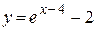 . .
|
6. а) 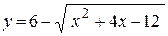 ; ;
| б) 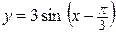 . .
|
7. а) 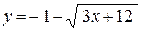 ; ;
| б) 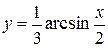 . .
|
8. а) 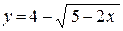 ; ;
| б) 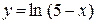 . .
|
9. а) 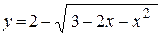 ; ;
| б) 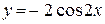 . .
|
10. а) 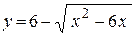 ; ;
| б) 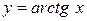 . .
|
11-20. Вычислить пределы:
11. а) 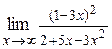 ; ;
| б) 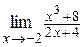 ; ;
| в) 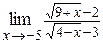 ; ;
| |
г) 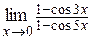 ; ;
| д) 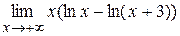 . .
| ||
12. а) 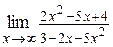 ; ;
| б) 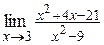 ; ;
| в) 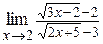 ; ;
| |
г)  ; ;
| д) 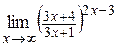 . .
| ||
13. а) 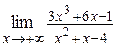 ; ;
| б) 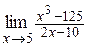 ; ;
| в) 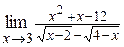 ; ;
| |
г) 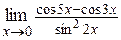 ; ;
| д) 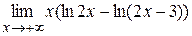 . .
| ||
14. а) 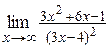 ; ;
| б) 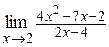 ; ;
| в) 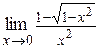 ; ;
| |
г) 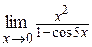 ; ;
| д) 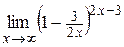 . .
| ||
15. а) 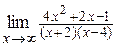 ; ;
| б) 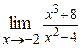 ; ;
| в) 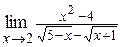 ; ;
| |
г) 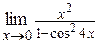 ; ;
| д) 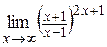 . .
| ||
16. а) 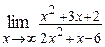 ; ;
| б) 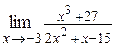 ; ;
| в) 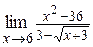 ; ;
| |
г) 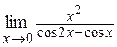 ; ;
| д) 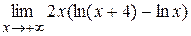 . .
| ||
17. а) 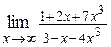 ; ;
| б) 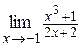 ; ;
| в) 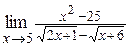 ; ;
| |
г) 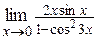 ; ;
| д) 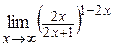 . .
| ||
18. а) 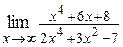 ; ;
| б) 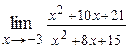 ; ;
| в) 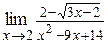 ; ;
| |
г) 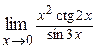 ; ;
| д) 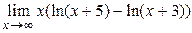 . .
| ||
19. а) 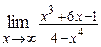 ; ;
| б) 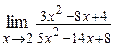 ; ;
| в) 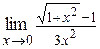 ; ;
| |
г) 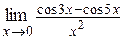 ; ;
| д) 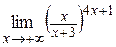 . .
| ||
20. а) 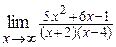 ; ;
| б) 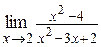 ; ;
| в) 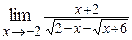 ; ;
| |
г)  ; ;
| д)  . .
| ||
21-30. Найти первые производные функций. В заданиях а) и б)дополнительно найти вторые производные.
21. a) 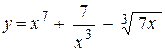 ; ;
| г) 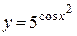 ; ;
|
б) 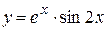 ; ;
| д) 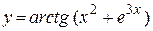 ; ;
|
в) 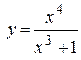 ; ;
| е) 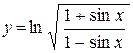 . .
|
22. a) 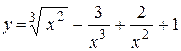 ; ;
| г) 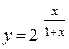 ; ;
|
б) 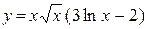 ; ;
| д) 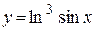 ; ;
|
в) 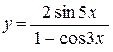 ; ;
| е) 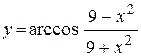 . .
|
23. а)  ; ;
| г) 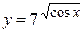 ; ;
|
б) 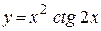 ; ;
| д) 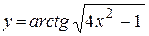 ; ;
|
в) 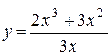 ; ;
| е) 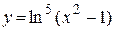 . .
|
24. а)  ; ;
| г)  ; ;
|
б) 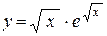 ; ;
| д) 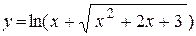 ; ;
|
в) 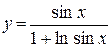 ; ;
| е) 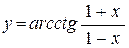 . .
|
25. а)  ; ;
| г) 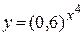 ; ;
|
б)  ; ;
| д) 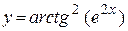 ; ;
|
в) 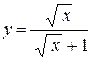 ; ;
| е) 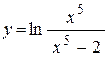 . .
|
26. а) 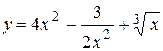 ; ;
| г)  ; ;
|
б) 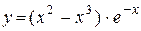 ; ;
| д) 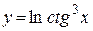 ; ;
|
в)  ; ;
| е) 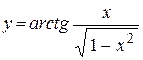 . .
|
27. а) 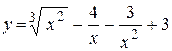 ; ;
| г) 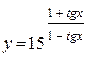 ; ;
|
б) 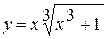 ; ;
| д) 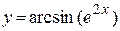 ; ;
|
в) 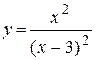 ; ;
| е) 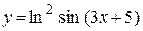 . .
|
28. а) 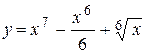 ; ;
| г) 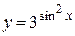 ; ;
|
б) 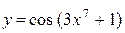 ; ;
| д) 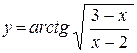 ; ;
|
в) 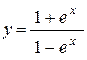 ; ;
| е) 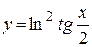 . .
|
29. а) 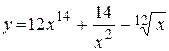 ; ;
| г)  ; ;
|
б) 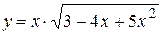 ; ;
| д) 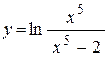 ; ;
|
в) 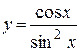 ; ;
| е) 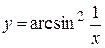 . .
|
30. а) 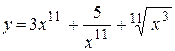 ; ;
| г) 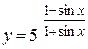 ; ;
|
б) 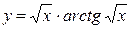 ; ;
| д) 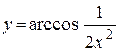 ; ;
|
в) 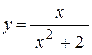 ; ;
| е) 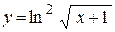 . .
|
31-40. Найти уравнение касательной к параболе, проходящей параллельно данной прямой. Сделать чертеж.
| 31. y = x2 – 4x + 3, y = 4x + 4. | 36. y = x2 + 2x – 3, y = – 4x + 2. |
| 32. y = – x2 – 2x + 3, y = –2x – 2. | 37. y = –x2 – 2x + 3, y = 4x – 3. |
| 33. y = x2 – 6x + 8, y = 6x + 1. | 38. y = x2 + 8x – 9, y = 4x. |
| 34. y = – x2 – 2x + 3, y = – 6x + 4. | 39. y = – x2 + 4x, y = 2x. |
| 35. y = x2 + 8x – 9, y = 2x + 1. | 40. y = x2 – 2x – 3, y = 6x + 3. |
41-50. Для функции, заданной параметрически, найти 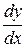 и
и 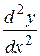 .
.
41. 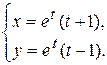
| 46. 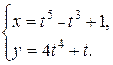
|
42. 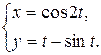
| 47. 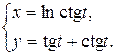
|
43. 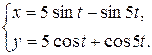
| 48. 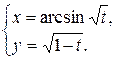
|
44. 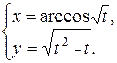
| 49. 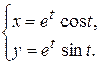
|
45. 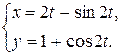
| 50. 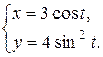
|
51-60. Найти значение 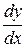 в точке
в точке 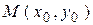 для функции, заданной неявно.
для функции, заданной неявно.
| 51. x2 + 2y2 + 6x – 4y – 13 = 0, M (1;-1). |
| 52. x3 – x y + y + 7 = 0, M (-1;-3). |
| 53. 3x2 – x y + y3 – x = 0, M (0;2). |
| 54. 3x2 – x y + y 2 +x – 34 = 0, M (-2;4). |
| 55. x2 y2 – 4y3 – x = 4, M (0;-1). |
| 56. x 6 + y 6 – 2xy = 0, M (1;1). |
| 57. 7x2 + x y – y3 + 3 = 0, M (1;-2). |
| 58. 2x2 – 9y2 + 4x + 18y + 11 = 0, M (2;-1). |
| 59. 3x2 – 5y2 – 6x – 20y + 25 = 0, M (2;1). |
| 60. 2x5 + y5 – 2xy + 26 = 0, M (1;-2). |
61-70. Вычислить пределы, используя правило Лопиталя.
61. а) 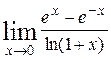 ; ;
| б) 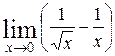 . .
|
62. а) 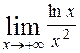 ; ;
| б) 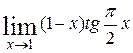 . .
|
63. а) 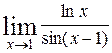 ; ;
| б) 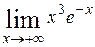 . .
|
64. а) 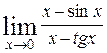 ; ;
| б) 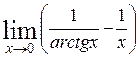 . .
|
65. а) 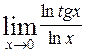 ; ;
| б) 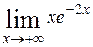 . .
|
66. а) 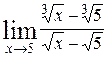 ; ;
| б) 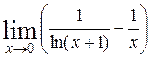 . .
|
67. а) 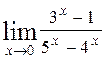 ; ;
| б) 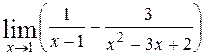 . .
|
68. а) 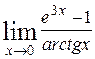 ; ;
| б) 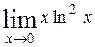 . .
|
69. а) 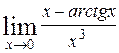 ; ;
| б) 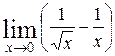 . .
|
70. а) 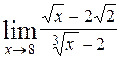 ; ;
| б) 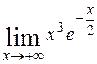 . .
|
81-90. Проверить справедливость равенства.
81. 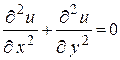 , если , если 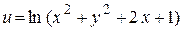 . .
|
82. 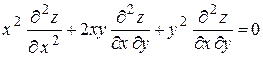 , если , если 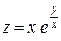 . .
|
83. 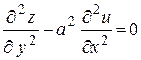 , если , если 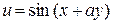 . .
|
84. 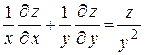 , если , если 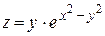 . .
|
85. 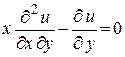 , если , если 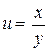 . .
|
86. 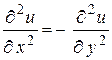 , если , если 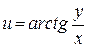 . .
|
87. 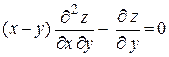 , если , если 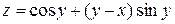 . .
|
88. 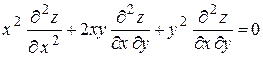 , если , если  . .
|
89. 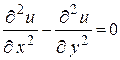 , если , если 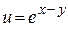 . .
|
90.  , если , если 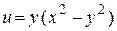 . .
|
91-100. Исследовать сходимость числовых рядов.
91. а) 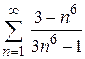 ; ;
| б) 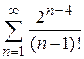 ; ;
| в) 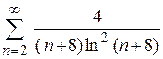 ; ;
|
г) 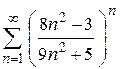 ; ;
| д) 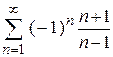 ; ;
| е) 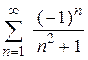 . .
|
92. а) 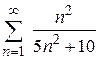 ; ;
| б) 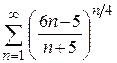 ; ;
| в) 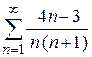 ; ;
|
г) 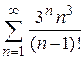 ; ;
| д)  ; ;
| е) 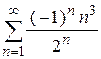 . .
|
93. а) 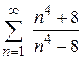 ; ;
| б) 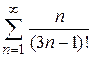 ; ;
| в) 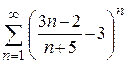 ; ;
|
г) 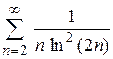 ; ;
| д) 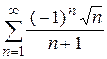 ; ;
| е) 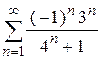 . .
|
94. а) 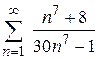 ; ;
| б) 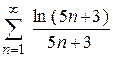 ; ;
| в) 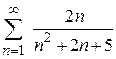 ; ;
|
г) 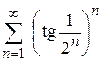 ; ;
| д) 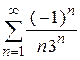 ; ;
| е) 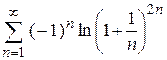
|
95. а) 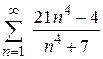 ; ;
| б) 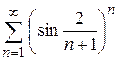 ; ;
| в) 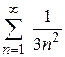 ; ;
|
г) 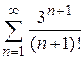 ; ;
| д) 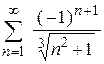 ; ;
| е) 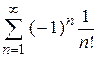 . .
|
96. а) 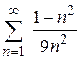 ; ;
| б) 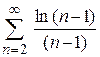 ; ;
| в) 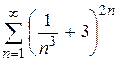 ; ;
|
г) 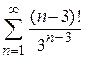 ; ;
| д) 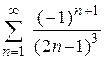 ; ;
| е) 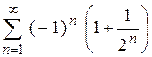 . .
|
97. а) 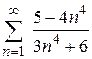 ; ;
| б) 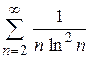 ; ;
| в) 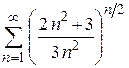 ; ;
|
г) 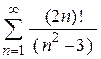 ; ;
| д) 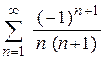 ; ;
| е) 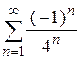 . .
|
98. а) 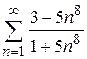 ; ;
| б) 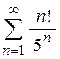 ; ;
| в) 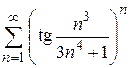 ; ;
|
г) 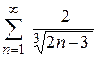 ; ;
| д) 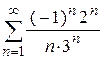 ; ;
| е) 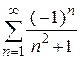 . .
|
99. а) 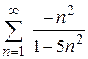 ; ;
| б) 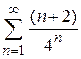 ; ;
| в) 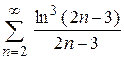 ; ;
|
г) 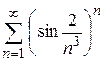 ; ;
| д) 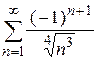 ; ;
| е) 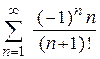 . .
|
100. а) 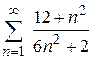 ; ;
| б) 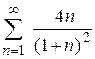 ; ;
| в) 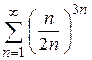 ; ;
|
г) 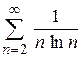 ; ;
| д) 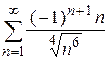 ; ;
| е) 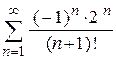 . .
|
101-110. Найти область сходимости степенного ряда.
101. 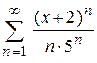 . .
| 102. 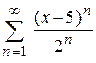 . .
| 103. 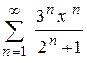
|
104. 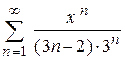 . .
| 105. 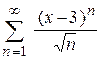 . .
| 106. 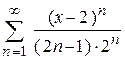 . .
|
107. 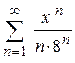 . .
| 108. 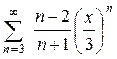 . .
| 109.  . .
|
110. 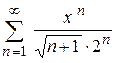 . .
|
Список литературы.
1. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1999.
3. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1987.
4. Шипачев В.С. Основы высшей математики. – М.: Высшая школа, 1994.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. – М.: Наука, 1978.
 2015-01-30
2015-01-30 799
799








