Математика
2семестр
для студентов всех специальностей
заочной формы обучения
Тюмень 2007
Утверждено редакционно-издательским советом
Тюменского государственного нефтегазового университета
Составители: Осташков В.Н., к.ф.–м.н., доцент
Скалкина М.А., к.ф.–м.н., профессор
Рожнова В.А., старший преподаватель
© государственное образовательное учреждение высшего профессионального образования
«Тюменский государственный нефтегазовый университет»
ПРЕДИСЛОВИЕ
Методические указания разработаны на кафедре высшей математики ТюмГНГУ на основании учебных планов и содержат вопросы теории и решения типовых примеров.
В методические указания включены следующие разделы высшей математики: введение в математический анализ, дифференциальное исчисление функций одной и двух переменных, числовые и степенные ряды.
Напоминаем, что решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
Введение в математический анализ.
1.1. Функции и их графики. Следующие функции действительной переменной называются основными элементарными функциями:
1. Постоянная функция: 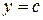 ,
, 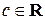 (рис. 1);
(рис. 1);
2. Степенная функция: 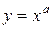 ,
, 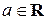 (рис. 2. a, 2. б, 2. в);
(рис. 2. a, 2. б, 2. в);
3. Показательная функция: 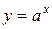 ,
, 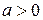 ,
, 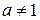 (рис. 3. a, 3. б);
(рис. 3. a, 3. б);
4. Логарифмическая функция: 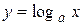 ,
, 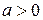 ,
, 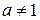 (рис. 4. a, 4. б);
(рис. 4. a, 4. б);
5. Тригонометрические функции: 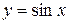 ,
, 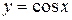 ,
, 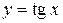 ,
, 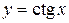 (рис 5. a, 5. б, 5. в, 5. г);
(рис 5. a, 5. б, 5. в, 5. г);
6. Обратные тригонометрические функции: 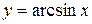 ,
, 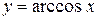 ,
,
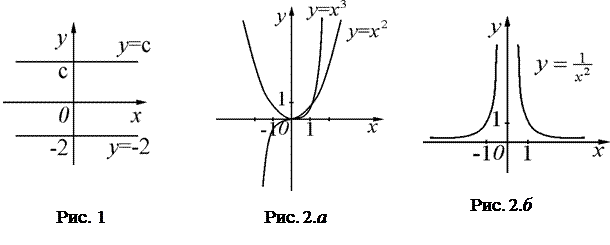
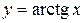 ,
, 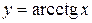 (рис. 6. a, 6. б, 6. в, 6. г).
(рис. 6. a, 6. б, 6. в, 6. г).
Графики элементарных функций:
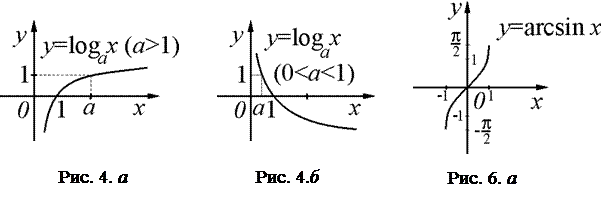 |  | ||
 |  | ||
Функция, полученная в результате последовательного выполнения композиции функций 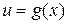 и
и 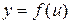 , называется сложной функцией:
, называется сложной функцией:
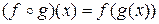 .
.
Элементарной функцией называется всякая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций, примененных к ним, и конечного числа их композиций.
Например, функция 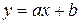 , где
, где 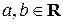 , называется линейной и является элементарной, так как она получена с помощью сложения двух функций, одна из которых получается путем умножения постоянной функции
, называется линейной и является элементарной, так как она получена с помощью сложения двух функций, одна из которых получается путем умножения постоянной функции 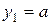 на степенную функцию
на степенную функцию 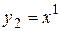 , вторая – постоянная функция
, вторая – постоянная функция 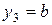 .
.
Область определения функции 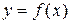 обозначают
обозначают 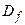 .
.
Графиком функции 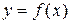 называется множество всех точек координатной плоскости
называется множество всех точек координатной плоскости 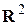 с координатами (
с координатами (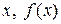 ), причем аргумент
), причем аргумент 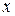 пробегает всю область определения
пробегает всю область определения 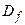 .
.
При построении графиков функции часто используют следующие простые геометрические рассуждения. Если Г - график функции 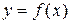 , то:
, то:
1) график функции 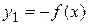 есть зеркальное отражение графика Г относительно оси
есть зеркальное отражение графика Г относительно оси 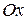 ;
;
2) график функции 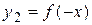 - зеркальное отражение графика Г относительно оси
- зеркальное отражение графика Г относительно оси 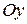 ;
;
3) график функции 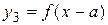 - смещение графика Г вдоль оси
- смещение графика Г вдоль оси 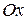 на величину а;
на величину а;
4) график функции 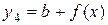 - смещение графика Г вдоль оси Oy на величину
- смещение графика Г вдоль оси Oy на величину 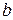 .
.
5) график функции 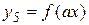 ,
, 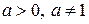 – сжатие графика Г в
– сжатие графика Г в 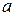 раз (при
раз (при 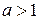 ) или растяжение в
) или растяжение в 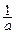 раз (при
раз (при 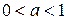 ) вдоль оси
) вдоль оси 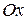 ;
;
6) график функции 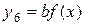 ,
, 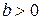 ,
, 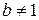 – растяжение графика Г в b раз (при
– растяжение графика Г в b раз (при 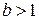 ) или сжатие в
) или сжатие в 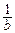 раз (при
раз (при 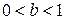 ) вдоль оси
) вдоль оси 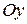 .
.
Пример 1. Найти область определения для данных функций и построить их графики.
а) 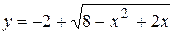 ; б)
; б) 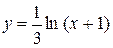 .
.
Решение. а) Функция определена, если 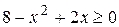 или
или 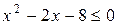 . Так как корни уравнения
. Так как корни уравнения 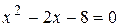 равны
равны 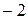 и
и 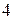 , неравенство справедливо в отрезке
, неравенство справедливо в отрезке 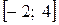 .
.
Итак, 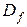 :
: 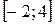 , значения функции
, значения функции 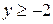 . Составим таблицу значений функции и построим ее график
. Составим таблицу значений функции и построим ее график
 | -2 | -1 | |||||
 | -2 | 0,2 | 0,8 | 0,8 | 0,2 | -2 |
Нетрудно видеть, что 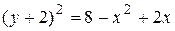 ,
, 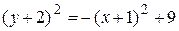
или 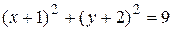 – это окружность с центром в точке
– это окружность с центром в точке 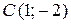 , радиусом
, радиусом 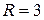 . Так как
. Так как 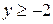 графиком данной функции является верхняя половина этой окружности (см. рис.7. а).
графиком данной функции является верхняя половина этой окружности (см. рис.7. а).
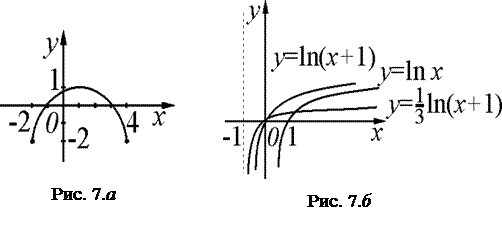 |
б)Логарифмическая функция определена для положительных аргументов, т. е.
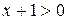 , значит
, значит 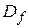 :
: 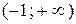 . График можно построить, преобразовывая график функции
. График можно построить, преобразовывая график функции 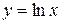 , т.е. сместив его влево на 1 и сжав в 3 раза вдоль оси
, т.е. сместив его влево на 1 и сжав в 3 раза вдоль оси 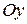 (см. рис. 7. б).
(см. рис. 7. б). 1.2. Предел функции. При вычислении предела функции 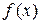 обычно руководствуются следующими соображениями:
обычно руководствуются следующими соображениями:
1) для всякой элементарной функции 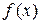 справедливо равенство
справедливо равенство 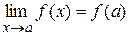 при любых
при любых 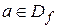 ;
;
2) если 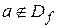 и функция
и функция 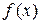 определена в некоторой окрестности точки
определена в некоторой окрестности точки 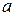 , то вычисление предела (раскрытие неопределенностей вида
, то вычисление предела (раскрытие неопределенностей вида 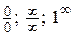 ) – достаточно сложная задача. Рассмотрим типичные случаи.
) – достаточно сложная задача. Рассмотрим типичные случаи.
1. Рациональные функции. Если рациональная функция имеет вид
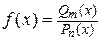 ,
,
где 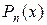 и
и 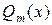 - некоторые многочлены, причем
- некоторые многочлены, причем 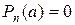 , то возможны два случая:
, то возможны два случая:
а) 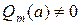 , тогда
, тогда 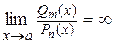 ;
;
б) 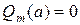 ; в этом случае непосредственная подстановка
; в этом случае непосредственная подстановка 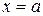 в дробь
в дробь 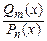 приводит к неопределенности, которую мы будем условно записывать так:
приводит к неопределенности, которую мы будем условно записывать так: 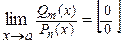 . Для раскрытия неопределенности, как правило, приходится разлагать числитель и знаменатель на множители и сокращать на линейный множитель
. Для раскрытия неопределенности, как правило, приходится разлагать числитель и знаменатель на множители и сокращать на линейный множитель  .
.
Примечание. Если  , то
, то  принадлежит области определения
принадлежит области определения 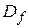 функции
функции 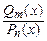 , и поэтому ее предел в точке
, и поэтому ее предел в точке 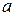 равен значению функции:
равен значению функции:
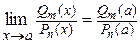 .
.
Пример 2. Вычислить: 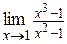 .
.
Решение. 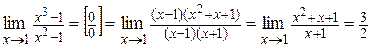 .
.
2. Иррациональные функции. Если неопределенное выражение содержит иррациональность, то, умножая на сопряженное выражение числитель и знаменатель, переводят иррациональность из знаменателя в числитель или наоборот.
Пример 3. Вычислить: 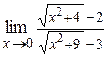 .
.
Решение. 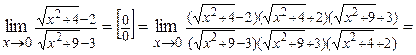
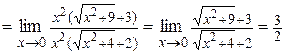 .
.
3. Предел при 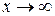 . При вычислении предела при
. При вычислении предела при 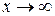 в рациональных или иррациональных выражениях может возникнуть неопределенность вида
в рациональных или иррациональных выражениях может возникнуть неопределенность вида 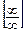 . Эту неопределенность раскрывают делением числителя и знаменателя на наивысшую степень
. Эту неопределенность раскрывают делением числителя и знаменателя на наивысшую степень 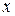 , входящую в выражение.
, входящую в выражение.
Пример 4. Вычислить 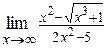 .
.
Решение. 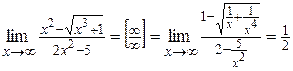 .
.
4. Первый замечательный предел, т.е. предел вида
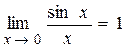
используется при раскрытии неопределенностей вида 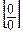 в тригонометрических выражениях.
в тригонометрических выражениях.
Пример 5. Вычислить 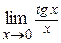 .
.
Решение. 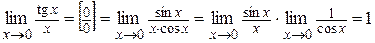 .
.
Пример 6. Вычислить 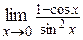 .
.
Решение. 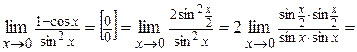
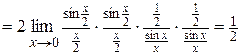 .
.
5. Второй замечательный предел, т.е. предел вида
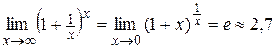
используют при вычислении пределов вида 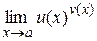 , где
, где 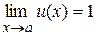 ,
, 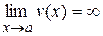 (что дает неопределенность вида
(что дает неопределенность вида 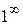 ).
).
Пример 7. Вычислить 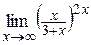 .
.
Решение. 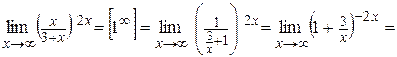
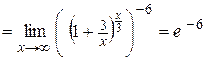 .
.
 2015-01-30
2015-01-30 1429
1429







