| Нулевая гипотеза Н0 | Дополни-тельные условия | Критерий – используемая статистика (выборочная характеристика) | Используемые распределение и таблица (Прил.) | Гипо-теза Н1 | Критическая область (КО) и формулы для нахождения её границ | Гипотеза Н0 не отвергается, если: | ||
1.
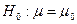
| 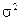 известна
известна
| 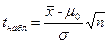
| Нормальный закон. Функция Лапласа 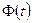 (табл.1)
(табл.1)
| 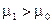
| ПКО | 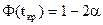
| 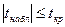
| |
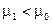
| ЛКО | |||||||
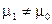
| ДКО | 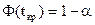
| ||||||
2.
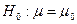
| 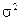 не
известна не
известна
| 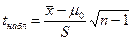
| Стьюдента 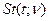
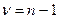 (табл.2)
(табл.2)
| 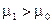
| ПКО | 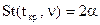
| 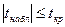
| |
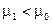
| ЛКО | |||||||
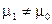
| ДКО | 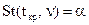
| ||||||
3.
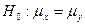
| 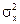 и и 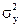 известны известны
| 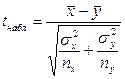
| Нормальный закон.
Функция Лапласа 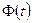 (табл.1)
(табл.1)
| 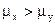
| ПКО | 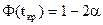
| 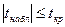
| |
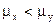
| ЛКО | |||||||
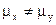
| ДКО | 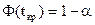
| ||||||
4.
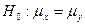
| 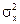 и и 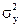 не
известны,
но равны не
известны,
но равны
| 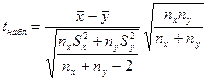
| Стьюдента 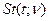
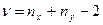 (табл.2)
(табл.2)
| 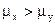
| ПКО | 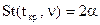
| 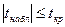
| |
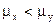
| ЛКО | |||||||
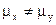
| ДКО | 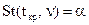
| ||||||
5.
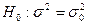
| 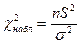
| Пирсона
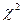
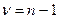 (табл.3)
(табл.3)
| 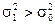
| ПКО | 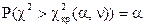
| 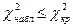
| ||
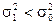
| ЛКО | 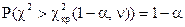
| 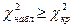
| |||||
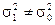
| ДКО | 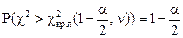
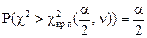
| 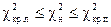
| |||||
6.
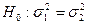
|
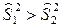
| 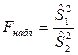 ; ;
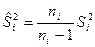
| Фишера-Снедекора 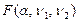
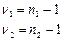 (табл.4)
(табл.4)
| 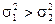
| ПКО | 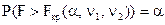
| 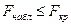
| |
7. 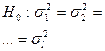 l – число генеральных совокупностей
l – число генеральных совокупностей
| 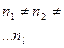
| Критерий Бартлетта
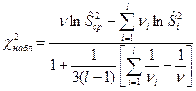 ; ;
| Пирсона
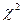
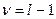 (табл.3)
(табл.3)
| ПКО | 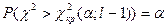
| 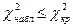
| ||
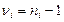 ; ;
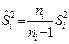 ; ;
| 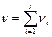 ; ;
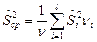
| |||||||
8. 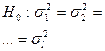 l – число генеральных совокупностей
l – число генеральных совокупностей
| 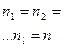
| Критерий Кохрана
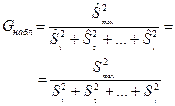
| G -распределение 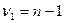 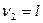 (табл.9)
(табл.9)
| ПКО | 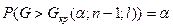
| 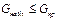
| ||
9.
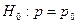
| 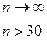
| 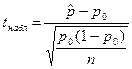 ; ;
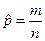
| Нормальный закон.
Функция Лапласа 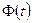 (табл.1)
(табл.1)
| 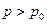
| ПКО | 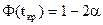
| 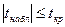
| |
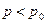
| ЛКО | |||||||
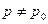
| ДКО | 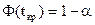
| ||||||
10.
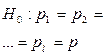 l – число генеральных совокупностей
l – число генеральных совокупностей
| 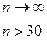
| 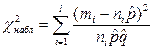 ; ;
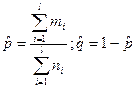 или
или
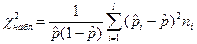 ; ;
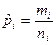
| Пирсона
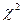
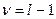 (табл.3)
(табл.3)
| ПКО | 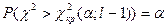
| 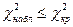
| ||
11.
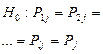
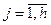 - группы - группы
| Полино-миальное распределение | 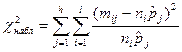
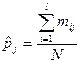
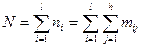
| Пирсона
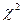
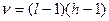 (табл.3)
(табл.3)
| ПКО | 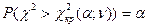
| 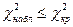
| ||
Правила проверки основных гипотез
|
|

Сейчас читают про:
 2015-01-30
2015-01-30 713
713







