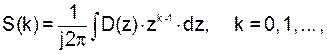Обращение (1) в общем виде даётся контурным интегралом

(2)

и позволяет вычислять значения последовательности S(k) по заданной функции D(z). Существует несколько способов нахождения обратного
z-преобразования (2) [2, 7]. В частности, элементы последовательности S(k) можно определить по формуле

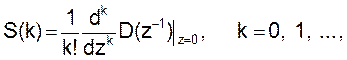(2а)

полагая 0! = 1.

Z-преобразование обладает рядом свойств, аналогичных преобразованию Фурье. Представим взаимосвязи (1) и (2) в символической форме S(k) ««D(z), тогда можно выделить следующие свойства:

а) если дано S _i (k) «D _i (z), i=1, 2, …, L, то для произвольных констант a _i имеем

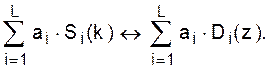
Это свойство характеризует линейность z-преобразования;

б) если дано S(k) «D(z), то

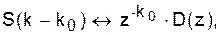
где k₀ – целое положительное число.

Здесь отражена теорема о сдвигах (задержках) сигнала. Она имеет важное следствие. Напомним, задержка непрерывного сигнала S(t – t₀) реализуется в цепи с коэффициентом передачи 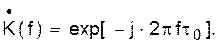Аналогично в дискретных системах задержка сигнала на k₀ отсчётов реализуется цепью с обобщённым коэффициентом передачи D(z) = z ^–ko;

в) если S _i (k) «D _i (k), i = 1, 2, то для свёртки (обозначено звёздочкой) этих последовательностей

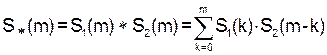(3)

имеем

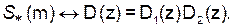(4)

В частности, автосвёртка последовательности S(k) (когда S₁(k) = S₂(k) =
= S(k)) даёт z-преобразование

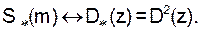(4а)

Эти свойства z-преобразования являются основными и позволяют решать разнообразные задачи по формированию и преобразованию дискретных сигналов.

В данном пособии изучаются процессы генерации дискретных сигналов и их свёрток. В основе используется следующая методика. Для произвольной ЛПП-системы (линейной с постоянными параметрами), показанной на рис.1, с системной функцией D(z) «g(k) свойства (3) и (4) z-преобразования проявляются следующим образом:

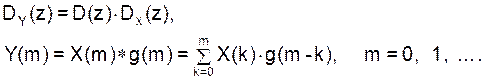(5)

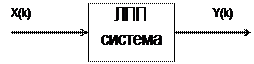Рис. 1

Это означает, что ЛПП-систему с импульсной характеристикой g(k) =
= S(k), k = 0, 1, …, можно рассматривать и как схему генерации сигна-
ла S(k). Действительно, её запуск единичным отсчетом в нулевой момент времени X(k)= d(k), где d(k) – символ Кронекера

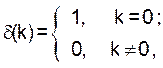(6)

даёт:

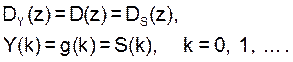(7)

Здесь учтено, что D_X(z) = 1. Другие варианты запуска X(k) позволяют получать комбинированные последовательности сигналов S(k) или их свёрток с заданными сигналами.

1.2. Общие принципы генерации сигналов

Общая блок-схема генератора сигналов представлена на рис.2. Она включает схему генерации заданной последовательности S₀(k) ограниченной длины (S₀(k) ¹ 0, k = 0 (1) N₀–1) и генератор запуска с выходом

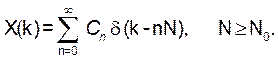
(8)

Это обеспечит генерацию “взвешенных” не перекрывающихся копий S₀(k):

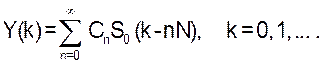(8а)

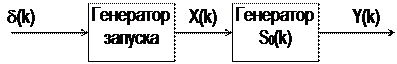
Рис.2

Возможные варианты запуска задаются последовательностью чисел C_n, n = 0, 1,..., и скважностью N/N₀ ≥ 1. В частности, последовательность C_n можно рассматривать как информационную (т.е. генератор запуска – это источник сообщения). В таком случае схема рис.2 имитирует передающее устройство с сигналами-переносчиками S₀(k).

Начнём с построения схемы генератора заданной последовательности S(k), k = 0, 1,....

Предварительно сделаем некоторые замечания.

В силу отображения S(k) «D(z) схема генератора должна следовать из (1). Но переменная z в этой записи – символическая и физического смысла не имеет. Представим (1) по схеме Горнера

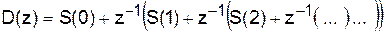(9)

и учтём свойство (б) z-преобразования. Теперь формально можно ввести схемный элемент z^–1 и трактовать его как оператор сдвига на один отсчёт. Возможные другие элементы схемы – сумматоры и умножители – очевидны.

Это же следует и из определения импульсной характеристики. Для воображаемого «генератора» она должна иметь вид

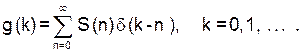(10)

Только в этом случае получим требуемую функцию

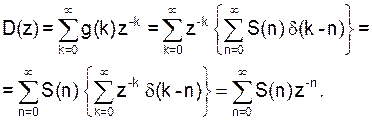
Теперь из (10) видно, что схема должна содержать элемент, реакцией которого на воздействие d(k) является d(k – n). Это и есть оператор сдвига на nотсчётов.

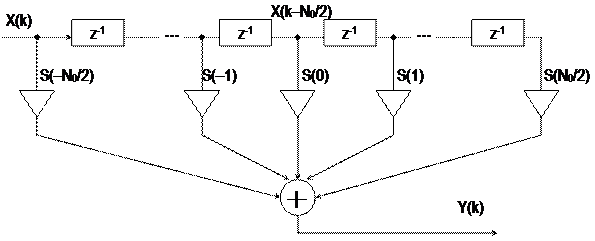
Итак, схема генератора (как ЛПП-система) может включать некоторый набор элементов, реализующих всего три операции: сдвига, умножения и сложения. Количество этих элементов определяется порядком полиномов, представляющих системную функцию. В теории дискретных систем рассматриваются различные варианты записи этих полиномов и, следовательно, представления схем [2, 4]. Задача заключается в выборе наиболее экономной схемы.

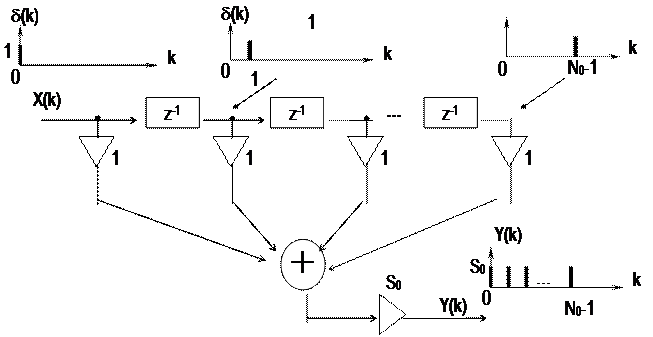
Во многих случаях выражение (1) удается представить в виде отношения полиномов с конечными степенями:

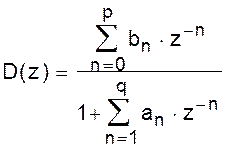. (11)

Соответствующая схема «генератора» последовательности Y(k) =
= S(k), k = 0, 1,... представлена на рис.3. Она включает элементы сдвига z^–1 на один отсчёт (регистры памяти), умножители на число (обозначено треугольником) и сумматор. Обратите внимание на знаки коэффициентов a_nв записи (11) и схеме – они обратные. Параметры a_n и b_nсхемы предварительно рассчитываются по конкретной последовательности данных S(k), k = 0, 1, …. Запуск схемы осуществляется в виде X(k) = d(k), см. (6).

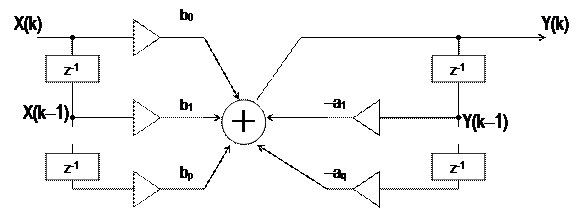Рис.3

Схему рис.3 называют прямой формой (формой №1) представления ЛПП-системы. В отличие от других форм она наглядно и просто отражает алгоритм формирования последовательности Y(k). Для этого достаточно выразить выход сумматора через его входы в текущий момент времени:

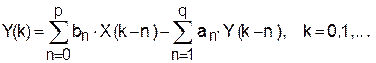(12)

с начальными условиями Y(k) = X(k) = 0, k < 0. В таком виде работу схемы рис.3 можно непосредственно моделировать на ЭВМ.

Структуру рис.3 с обратными связями еще называют рекурсивной схемой (или рекурсивным фильтром). Если обратные связи отсутствуют (а_n = 0, n = 1, 2,..., q), то все расчеты упрощаются. Параметры схемы и алгоритма (12) находятся непосредственно: b_n = S(n), n = 0, 1,..., p.

Примечание. В аналоговом варианте структуру рис.3 можно реализовать на многоотводных линиях задержки, усилителях и сумматоре. В цифровом варианте параметры a_n и b_n представляются кодами и все операции – это действия c кодами. В вырожденном случае, когда параметры a_n и b_n – нули и единицы (как одноразрядные числа в двоичной системе), схема и алгоритм (12) должны «работать» по правилам двоичной логики (сложение и умножение по mod 2). Подробнее об этом см. в подразд. 1.5.

1.3. Генераторы элементарных сигналов

Рассмотрим примеры построения генераторов элементарных сигналов.

1. Источник равномерной последовательности.

Положим, необходимо получить сигнал вида

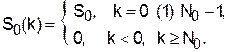(13)

Z-преобразование этого сигнала равно

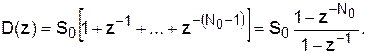(14)

Здесь учтены свойства геометрической прогрессии:

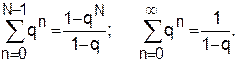(15)

Два варианта (14) системной функции D(z) реализуются соответствующими схемами (рис.4,а,б).

Запуск этих схем осуществляется дельта-функцией Кронекера d(k). Динамика работы показана эпюрами на схеме. Моделировать эти схемы можно по следующим алгоритмам, (см. 12):

а)

(16)

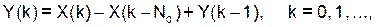б)

полагая на входе X(k) = d(k). Масштабный множитель S₀ в алгоритмах опущен.

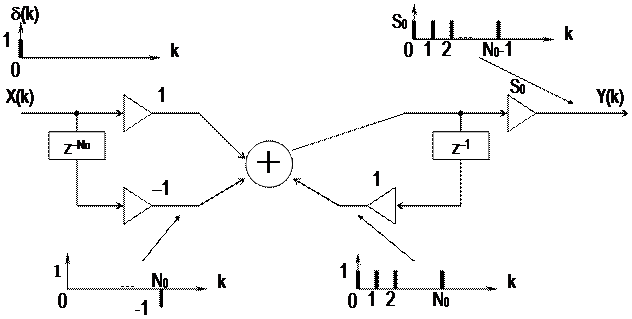
2. Источник убывающей (возрастающей) последовательности.

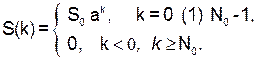Положим, генерируемый сигнал должен иметь вид

	(17)

а

б

Рис.4

Здесь а > 0. Z-преобразование сигнала равно, см. (15):

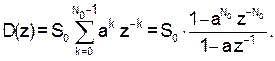(18)

В данном случае рекурсивный вариант схемы предпочтителен (содержит меньше различных множителей). Схема представлена на рис.5.

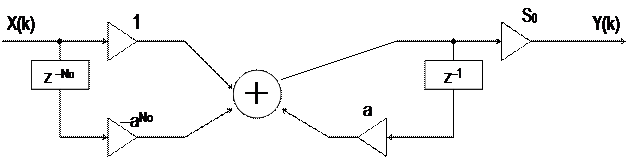Рис.5

Как видно, эта схема аналогична схеме, изображенной на рис.4,б, с той лишь разницей, что теперь в «кольце» рекурсивной части вместо 1 «крутится» число а, образуя на каждом такте степени в (17). Процесс прекращается на такте с номером k = N₀. Это обеспечивает нерекурсивная часть схемы. Алгоритм функционирования схемы задается равенством (масштабный множитель S₀ опущен)

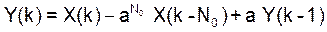(19)

с условием X(k)= d(k).

3. Источник гармонической последовательности.

Рассмотрим сигнал вида

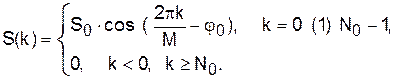(20)

Здесь М – число отсчётов на период гармонической функции, а весь сигнал включает n периодов: N₀ = n∙M.

Примечание. Формула (20) соответствует аналоговому варианту сигнала:

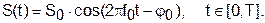Отрезок Т включает целое число (n) периодов гармонических функций:
n = T/T₀ = f₀∙T. Замена непрерывного времени на дискретное t ® k∙Δt, k = 0 (1) N₀–1 с учётом условий: N₀ = T/Δt = n∙T₀/Δt = n∙M дает дискретный вариант сигнала

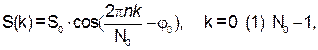c параметром (номером частоты): n = N₀/M = f₀∙T.

Перепишем (20) в иной форме:

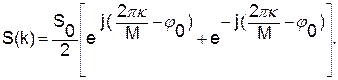
Теперь также можно использовать свойство геометрической прогрессии:

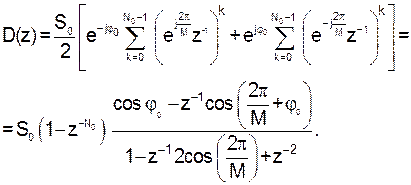(21)

Отсюда следует, что схема «генератора» включает две части (рис.6). Первая часть задаёт границы сигнала – по формуле (20). Вторую часть называют идеальным косинусным резонатором с параметрами:

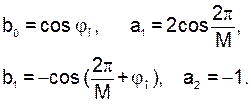(22)

Возбуждая его указанным способом, получаем дискретную гармоническую функцию заданной длины. Обратите внимание: здесь гарантированно значение начальной фазы φ₀. В аналоговых генераторах это недостижимо.

Рис.6

Моделируется схема, изображенная на рис.6, следующим образом (масштабный множитель S₀ oпущен):

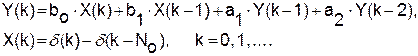(23)

Заметим: если менять параметры S₀, M или φ₀ сигнала (следовательно, и схемы) на тактах, кратных N₀, то получим эффекты модуляции (амплитудной, частотной и фазовой). Так, для имитации частотно-манипулированных сигналов достаточно менять два параметра схемы b₁ и a₁, см. (22).

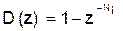В рассмотренных примерах можно выделить два характерных момента. Рекурсивная структура генератора (как более экономная) возможна только в случае, если последовательность S(k), k= 0 (1) N₀–1 образует геометрическую прогрессию. При этом границы последовательности фиксируются схемой с системной функцией

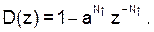(см. рис.4,б и рис.6) или как на рис.5:

Для некоторого класса сигналов (даже при наличии частичных геометрических прогрессий) нерекурсивная структура генератора остается безальтернативной. Это имеет место, например, в случаях четной или нечетной симметрии теоретической модели сигнала:

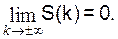c асимптотическим убыванием:

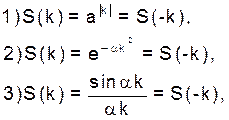Примерами могут служить последовательности:

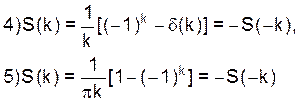
и др. Такие ряды часто встречаются в теории дискретных сигналов и цепей.

Основная проблема здесь – в «отрицательном» времени. Её можно обойти следующим образом.

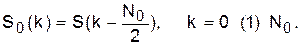Положим, необходимо генерировать усечённую последовательность 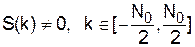, включающую N₀+1 отсчётов (N₀ – чётное). Чтобы исключить двустороннее z-преобразование, введём замену

(24)

Теперь проблема положительных степеней в z-преобразовании (т.е. «отрицательного» времени) исчезает:

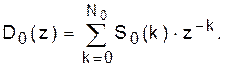
В соответствии с этим схема генератора принимает вид, представленный на рис.7. Параметры схемы b_n рассчитываются с учетом формулы (24): b_n =
= S₀(n), n = 0 (1) N₀. Наращивая в обе стороны от середины число звеньев схемы (т.е. увеличивая N₀), можно аппроксимировать теоретический сигнал S(k) с приемлемой точностью.

Рис.7

Работа схемы моделируется алгоритмом, см. (12):

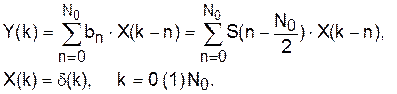(25)

Как нетрудно заметить, здесь Y(k) восстанавливает задержанную копию сигнала:

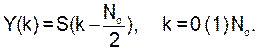
1.4. Генераторы запуска

Рассмотрим теперь возможные варианты построения генераторов запуска, приведенных на рис.2. Они позволяют имитировать различные системы управления и модуляции по формуле (8а).

Принцип построения таких генераторов аналогичен рассмотренным в п.1.2.

Для системной функции генератора запуска в соответствии с (8) имеем:

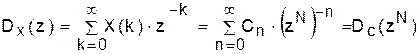. (26)

Итак, необходимо определить z-преобразование ряда C_n, n = 0, 1,...., и затем, вместо переменной z, использовать её степень z^N. Здесь есть ограничения: N ≥ N₀ (речь идёт о генерации редких отсчетов).

Рассмотрим примеры:

1. Периодический запуск (с периодом N отсчётов).

Полагаем С_n = 1, n = 0, 1,... Это даёт:

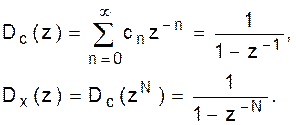(27)

Cхема генератора запуска представлена на рис. 8,а. Подав на её вход единичный отсчет δ (k), получим гребенку:

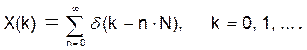(28)

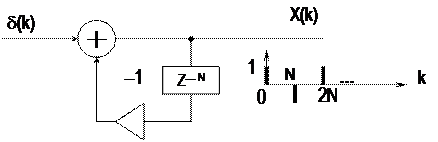
2. Знакопеременный запуск.

Пусть теперь C_n = (–1)ⁿ, n = 0, 1,... В этом случае имеем:

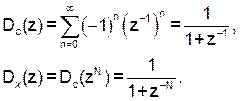(29)

Схема генератора показана на рис. 8,б. Запуск ее δ-функцией Кронекера даёт:

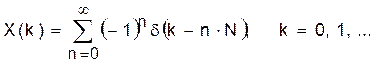. (30)

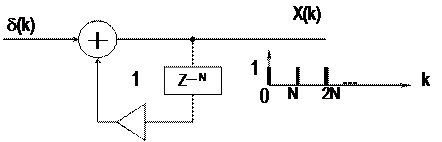Здесь также имеется периодичность, но с периодом 2N. Заметим, что при моделировании схем достаточно ограничиться в (28) и (30) конечным числом слагаемых.

а

б

Рис.8

1.5. Генерация кодовых последовательностей

Наряду с указанными схемами запуска возможны и другие варианты – с имитацией различных импульсных последовательностей из нулей и единиц типа кодовых.

Предварительно сделаем некоторые замечания по применению аппарата Z-преобразования к таким последовательностям.

Положим, что C_n, n = 0 (1) L–1 – это последовательность нулей и единиц как одноразрядных чисел в двоичной системе. Z-преобразование последовательности представляется полиномом (С_L–1=1):

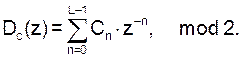(31)

По формальным признакам это преобразование ничем не отличается от общей формулы (1). Однако здесь необходимо учитывать следующее обстоятельство. Все операции (сложение, умножение) с полиномами такого вида сводятся к операциям над их коэффициентами. Поэтому свойства подобных полиномов и характер операций зависят от множества, которому принадлежат его коэффициенты. Так, в формуле (1) по умолчанию полагалось, что коэффициенты S(k) принадлежат множеству вещественных чисел (или его расширению – множеству комплексных чисел) с обычными арифметическими операциями (сложением, умножением). В формуле же (31) необходимо учитывать ограничения: коэффициенты С_n принадлежат множеству, состоящему всего из двух элементов – 0 и 1. Сложение и умножение элементов этого множества выполняется в виде арифметических операций по модулю 2 (в двоичной системе).

Итак, независимо от системы счисления для импульсных последовательностей С_n, n = 0 (1) L–1 должны выполняться все свойства (а, б, в)
z-преобразования (1). Сохраняются также правила обращения (2) и (2а). Следовательно, остаются в силе все приемы построения схем генераторов и соответствующих алгоритмов. Изменения (в формулах, схемах и алгоритмах) касаются только вида операций сложения и умножения. Операция сложения должна выполняться, как сложение по mod 2 (это и зафиксировано в формуле (31)). Операция же умножения фактически реализуется наличием (если С_n=1) или отсутствием (если С_n=0) соответствующего элемента в формуле, схеме или алгоритме.

Примечания: 1. В общем случае Р-ичной системы счисления одноразрядные числа С_n могут принимать значения 0, 1,..., Р–1. Кратко это записывается так: C_nÎGF(P), обозначая тем самым, что множество значений С_n принадлежит полю Галуа порядка Р (P – простое число) с арифметическими операциями по модулю mod P. При этом z-преобразование (31) называют полиномом над полем GF(P).

2. Перепишем (31), вводя положительные степени:

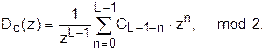
Сумма справа – это полином, представляющий некоторое кодовое слово
(С_L-1,..., C₁, C₀). Символы в кодовых словах располагают справа налево (от младшего к старшему разряду). В z-преобразовании (31) символы кодовых слов расположены в обратном порядке – по ходу «текущего» времени.

При переходе к схемам прежде всего обратим внимание на особенность операций с полиномами (31) в модульной арифметике.

Положим, дана последовательность из трёх элементов с = (1, 0, 1).
Z-преобразование последовательности можно представить в двух вариантах:

D_c(z) = 1+ z^–2 = (1 + z^–1)∙(1 + z^–1), mod 2. (32)

Проверить равенство несложно:

(1 + z^–1) (1 + z^–1) = 1+ (1 + 1) z^–1 + z^–2 =1 + z^–2, mod 2.

Второй вариант в (32) получен на основании теоремы о разложении многочленов на множители. Если z₁ и z₂ – корни уравнения D_c(z) = 0, то можно записать:

D_c(z) =1 + z^–2 = (1 + z²) / z² = ((z – z₁)∙(z – z₂)) / z².

В данном случае уравнение

1 + z² = 1 – z² = 0, mod 2,

имеет один корень (кратности 2): z₁ = z₂ = 1. Он и представлен в формуле (32).

Заметим, что в операции сложения по mod 2 знаки «+» и «–» тождественны, нет различия между (+1) и (–1).

На основании (32) можно составить две схемы генерации чисел с=
= (1, 0, 1). С учётом условия (26) генерации редких импульсов получим схемы, приведенные на рис. 9,а,б.

а б

Рис.9

Каскадная структура рис.9,б следует из представления системной функции D_c(z) в виде произведения.

Положим теперь, что импульсная последовательность С_n состоит только из одноразрядных единиц: С_n = 1, n =0, 1, …. В этом случае z-преобразование приводит к результатам, схожим с (15) для геометрических прогрессий:

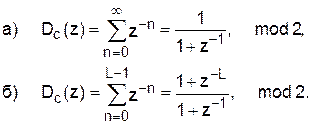(33)

Проверить эти равенства несложно. Достаточно раскрыть произведения и объединить члены с одинаковыми степенями z:

а) (1 + z^–1 + z^–2 +…)∙(1 + z^–1) = 1 + (1 + 1) z^–1 + (1 + 1) z^–2 + …= 1, mod 2;

б) (1 + z^–1 + z^–2 +… + z^–L+1)∙(1 + z^–1) = 1+ (1 + 1)∙z^–1 + … + (1 + 1) z^–L+1 + z^–L =

= 1 + z^–L, mod 2.

В соответствии с (33) схемы запуска принимают вид, показанный на рис.10. Здесь также учтено условие (26) N-кратных интервалов между единицами.

а б

Рис.10

Обратите внимание на подобия и отличия в схемах рис.4, 8 и 10: непрерывную генерацию обеспечивает рекурсивная часть схемы; границы последовательностей задаются нерекурсивной частью; в случае одноразрядных сумматоров (по mod 2) множитель (–1), как отмечалось, опускается.

Работа схем рис.10 моделируется следующими рекуррентными уравнениями:

а) x (k) = d (k) + x (k – 1), mod 2,

k = 0, 1, …; (34)

б) x (k) = d (k) + d (k – LN) + x (k – N), mod 2,

k = 0, 1, ….

В рассмотренных примерах последовательность С_n носила регулярный характер. Для имитации передаваемых сообщений желательно формировать некоторую псевдослучайную импульсную последовательность. Примером может служить так называемая М-последовательность. Кратко рассмотрим способы формирования таких последовательностей.

М-последовательность задаётся рекуррентным соотношением:

С_n = a₁ С_n–1 + a₂ С_n–2 + … + С_n–m, mod 2, (35)

n = 0, 1, …; С_n = 0, n < 0.

Вид последовательности определяется конкретным набором (a₁, a₂, …, a_m–1) двоичных чисел и значением m.

Примечание. Приведём примеры типичных рекуррентных последовательностей:

— геометрическая прогрессия С_n = q∙С_n–1, n = 0, 1, …, и её вырожденный случай в (33) со знаменателем q = 1 и С₀ = 1;

— числа Фибоначчи в обычной арифметике

С_n = С_n–1 + С_n–2, n = 0, 1, …, С₀ = 1, (это ряд 1, 1, 2, 3, 5, 8, …)

и их двоичный аналог С_n = С_n–1 + С_n–2, mod 2, n = 0, 1, …, С₀ = 1,

(это ряд 1, 1, 0, 1, 1, 0 …).

Схема генерации чисел Фибоначчи и ее обобщение рассмотрены в прил. 1.

В силу ограниченности значений a и m всегда можно ожидать, что с некоторого момента n значения С_n начнут повторяться. Это означает, что последовательность (35) обладает периодичностью: С_n = С_n+L. Выбором ко-эффициентов a₁, …, a_m–1 (при заданном m) можно обеспечить максимально возможное значение периода

L = 2^m – 1. (36)

Отсюда и название: последовательность максимальной длины. Она включает 2^m–1 единиц и 2^m–1 – 1 нулей. Внешне кажется, что нули и единицы расставлены хаотически с примерно равными вероятностями. В связи с этим такие последовательности называют псевдослучайными.

Фактически (35) является алгоритмом работы генератора М-последовательности. Необходимо только обеспечить запуск этого генератора. Как и во всех рассмотренных выше случаях, для запуска введём единичный отсчёт:

С_n = d(n) + a₁∙С_n–1 + a₂∙С_n–2 + … + С_n–m, mod 2 (37)

Теперь начальное значение последовательности определено: С₀ = d(0) = 1. Остаётся найти системную функцию генератора.

Перепишем (37), разделив вход и выход знаком равенства:

d(n) = С_n + a₁∙С_n–1 + a₂∙С_n–2 + … + С_n–m, mod 2, (37а)

и выполним z-преобразование обеих частей. Пусть D_c(z) –
z-преобразование последовательности С_n, n = 0, 1, …: С_n «D_c(z). С учётом свойства (б) z-преобразования

С_n–1 «z^–1 D_c(z),

С_n–m «z^–m D_c(z),

для (37а) получим:

D_вх(z) = D_вых(z) = D_c(z)∙(1 + a₁ z^–1 + … + z^–m).

Z-преобразование левой части в (37а) определено: D_вх(z) = 1. Отсюда следует, что системная функция генератора равна:

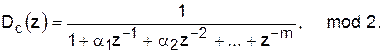(38)

Эта форма реализуется рекурсивной схемой, которая будет генерировать периодическую последовательность двоичных чисел. Как отмечалось, максимального периода L, см. (36), можно достичь только определенными обратными связями (коэффициентами a₁, …, a_m–1).

Для генерации М-последовательности без периодического повторения в (37) необходимо ввести дополнительный элемент d(n–L). Он задаёт верхнюю границу ряда С_n. В этом случае вместо (37а) запишем:

d(n) + d(n–L) = С_n + a₁ С_n–1 + a₂ С_n–2 + … + С_n–m, mod 2.

После Z- преобразования получим новую системную функцию генератора:

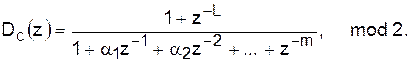(39)

Нерекурсивная часть генератора (числитель в (39)) обеспечит формирование М-последовательности заданной длины L.

И последнее замечание. Если выполнить деление числителя на знаменатель в (39), то получим многочлен степени L–m. Это будет системная функция эквивалентного генератора М-последовательности без рекурсивной части.

Примечания: 1. В теории кодирования равенства вида (37а) называют «правилом проверки на чётность»: правая часть должна содержать чётное число единиц, сложение которых (по mod 2) даёт нуль (при n > 0).

2. Значение L по (36) реализуется только при выполнении двух условий:
а) степенной полином в знаменателе (38) должен быть «неприводимым», т.е. не представляться множителями; б) этот же полином должен быть «примитивным», т.е. являться делителем двучлена 1 + z^–L (деление в (39) должно быть без остатка). Таблицы таких полиномов для различных степеней m = 2, 3, 4, … можно найти в литературе по кодированию [8].

Рассмотрим все указанные варианты построения генераторов
М-последовательностей на примере полиномов степени m = 4. В этом случае L= 15. Запишем все неприводимые множители полинома 1 + z^–15 [8]:

1 + z^–15 = (1 + z^–1)∙(1 + z^–1+ z^–2)∙(1 + z^–3+ z^–4)∙(1 + z^–1+ z^–4)х

х(1 + z^–1+ z^–2+ z^–3 + z^–4), mod 2. (40)

Здесь только три полинома степени m = 4 (третий, четвертый и пятый). Но последний полином является также и делителем полинома 1+z^–5, см. формулу (33), т.е. он будет порождать последовательность из пяти элементов. Таким образом, для формирования М-последовательности из 15 элементов можно использовать только третий и четвертый полиномы.

Запишем системную функцию генератора в общем виде:

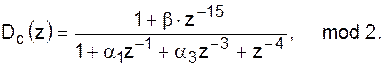(41)

Соответствующая схема представлена на рис.11. Сумматор здесь – по mod 2.

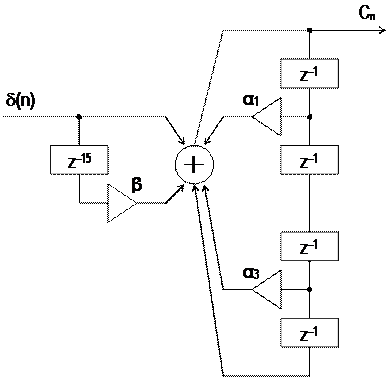Рис.11

Схема работает в двух режимах:

а) b = 0 – генерация периодической М-последовательности с L=15 элементами;

б) b = 1 – генерация одного периода М-последовательности.

Коэффициенты a устанавливаются в соответствии с порождающим полиномом. В первом варианте (для полинома 1 + z^–3 + z^–4) имеем: a₁ = 0, a₃ = 1. Схема генерирует последовательность С_n по алгоритму:

С_n = d(n) + С_n–3 + С_n–4, mod 2, n =0, 1, ….

В результате получим (для одного периода):

С_n = (1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0). (42)

Во втором варианте (для полинома 1 + z^-1 + z^–4) имеем a₁=1, a₃=0. Схема рис.11 формирует последовательность С_n по алгоритму:

С_n = d(n) + С_n–1 + С_n–4, mod 2, n =0, 1, ….

Результатом (для одного периода) будет:

С_n = (1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0). (43)

Как отмечалось, схему генератора можно реализовать и в нерекурсивном варианте. Для этого достаточно составить цепочку из 12 элементов сдвига z^–1 и объединить ее вход и выходы в соответствии с ненулевыми позициями кода (42) или (43). Последние три позиции дополняются искусственно. Ясно, что ценность таких схем мала, особенно для больших значений L.

Для перевода генератора М-последовательности в схему запуска необходимо заменить элементы z^–1 и z^–L на z^–N и z^–LN (как на рис.9 и 10). В результате получим последовательность редких импульсов X(k):

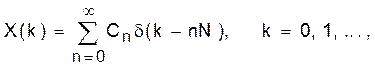
следующих с интервалом в N тактов. При этом символические значения кода С_n (1 или 0) переводятся в однополярные импульсы.

В технических задачах наряду с однополярными импульсами используются и двухполярные. Для этого достаточно ввести промежуточное преобразование:

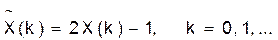. (44)

Теперь последовательность 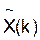будет менять знак в соответствии с кодом С_n.

Различия этих разновидностей импульсов можно заметить на примере запуска генератора «радиоимпульсов» (см. рис. 6). Однополярный запуск имитирует кодированный АМ-сигнал, а двухполярный – кодированный ФМ-сигнал.

1.6. Свёртка дискретных сигналов

Общую схему генерации сигналов (см. рис.2) можно видоизменить, сняв ограничения на интервалы следования импульсов запуска N ≥ N₀.

Теперь блок-схема, приведенная на рис.12, представляет последовательно соединенные линейные системы.

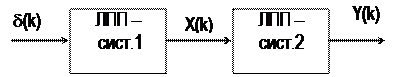Рис.12

Системная функция всей схемы равна, см. (4):

D_y(z) = D₁(z) D₂(z).

Такая схема допускает различные интерпретации. Если определены импульсные характеристики систем: g₁(k) = S₁(k) = X(k) и g₂(k) = S₂(k), то речь идёт либо о фильтрации сигнала:

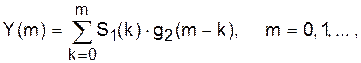(45)

либо о формировании нового сигнала по правилу:

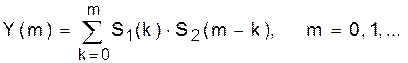. (45а)

В обоих случаях основной операцией является дискретная свёртка. Процедура по схеме рис.2 относится к вырожденному случаю свёртки.

Для свёрток, как линейных операций, действуют те же правила
z-преобразований. В частности, выполняется формула обращения (2а).

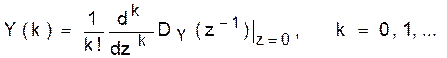. (46)

Она может служить контрольным тестом для проверки результатов
свертки.

Механизмы формирования дискретной свёртки покажем графически на примере двух сигналов, ненулевые значения которых равны:

S₁(k) =1, k = 0, 1, 2; S₂(k) = k + 1, k = 0, 1. (47)

На рис.13,а показаны все этапы формирования свёртки по формуле (45). Она отражает принцип суперпозиции в линейных системах: реакция на сумму воздействий равна сумме реакций на каждое воздействие. На эпюрах показаны сигнал S₁(k) (генерируемый первой системой), реакции второй системы на
каждый из отсчётов входного сигнала и их сумма Y(m).

Другой механизм следует из (45а). Здесь перемножаются отсчёты двух сигналов, один из которых, например S₂(k), обращен во времени. На рис.13,б показаны все сдвиги обращённой копии сигнала S₂(k). Для каждого значения m выполняется умножение отсчётов S₁(k)∙S₂(m–k) и суммирование по всем k. Результатом будет свёртка Y(m).

б

а

Рис.13

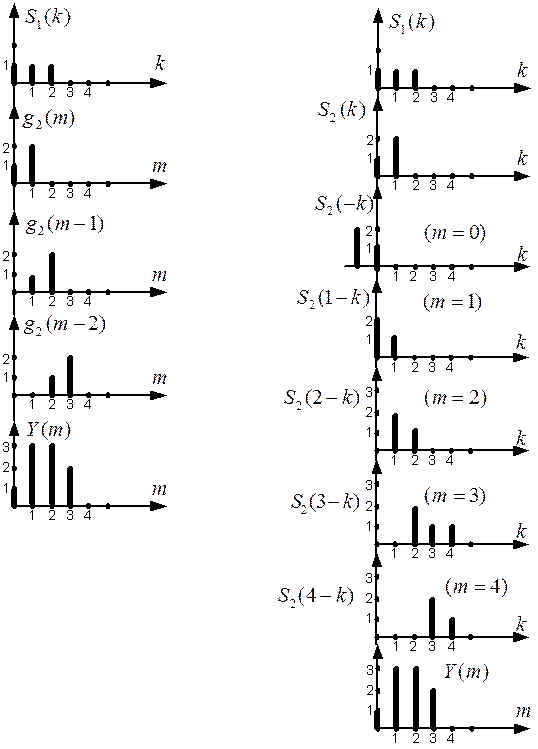Для проверки вычислений используем правило обращения (46). Предварительно найдем системные функции 1- и 2-й ЛПП-систем для сигналов (47):

(48)

Здесь z-преобразования определены по (15) и (1). Теперь системная функция всей схемы рис.12 явно определена:

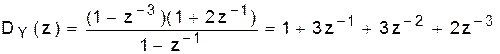. (49)

Её подстановка в (46) дает:

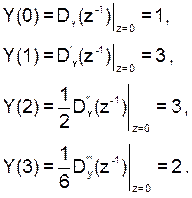
Независимые проверки можно выполнить по схемам и алгоритмам генерации свертки Y(k) = S₁(k) 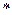S₂(k).

Из (49) следуют два варианта схемы генерации последовательности Y(k) (рис.14). Вариант 14,а – с совмещённым элементом сдвига z^–1 (он входит в рекурсивную и нерекурсивную части, см. первую запись в (49)). Схема рис.14,б – нерекурсивный вариант (с большим числом множителей).

Работа схем рис.14 моделируется алгоритмами:

а) Y(k) = X(k) + 2X(k – 1), k = 0, 1, …,

X(k) = d(k) – d(k – 3) + X(k – 1),

X(k) = Y(k) = 0, k<0;

б) Y(k) = d(k) + 3d(k – 1) + 3d(k – 2) + 2d(k – 3).

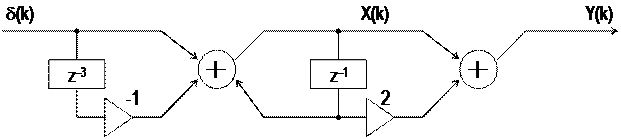а

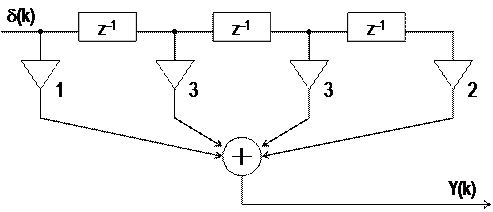б

Рис.14

В табл.1 приведены все состояния схемы рис.14,а для текущего времени k = 0, 1, ….

Таблица 1

k	X(k)	Y(k)

Примечание. Для линейных систем порядок расположения звеньев не влияет на результат работы схемы. Это следует из равенства

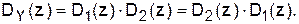
Изменения проявляются только на промежуточных эпюрах рис.13, схеме рис.14,а и алгоритме её работы. Проверьте!

На приведённом примере можно заметить характерное свойство свёрток: её протяжённость превышает протяжённость любого из свёртываемых сигналов. Это свойство формулируется следующим образом. Для свёртываемых сигналов с числом ненулевых отсчетов: N_i, i =1, 2, число ненулевых отсчётов свёртки равно N₁+N₂–1.

Данную особенность необходимо иметь в виду при формировании периодической свертки Y(k) = Y(k + N). Период N свёртки должен быть ограничен снизу: N ≥ N₁ + N₂. Это исключает наложение периодических копий сигнала.

В качестве иллюстрации на рис.15 приведена дополненная схема (см. рис.14,а) генерации свёртки с периодом в N = 5 тактов.

Рис.15

Левая часть схемы (выход первого сумматора) является генератором запуска. Она формирует периодическую гребенку d_N(k) функций Кронекера (рис.16,а). В результате получим периодическую свёртку (рис. 16,б). Заметим, что с помощью генератора запуска можно менять как полярность копий свёрток, так и период их следования (см. подразд.1.4).

Рис.16

Правила свёртки позволяют представлять сложные сигналы в виде композиции элементарных сигналов. Так, например, все вариации формы сигнала от трапецеидальной до треугольной можно получить свёрткой двух равномерных последовательностей (13), меняя лишь соотношения между их длительностями N₁ и N₂. При N1 = N2 получим автосвёртку, т.е. сигнал треугольной формы.

Особо здесь отметим практически важный случай. Положим, необходимо создать дискретную модель прямоугольного видеоимпульса

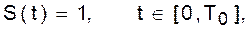(50)

с условием, что на отрезке T₀ должно уложиться целое число отсчётов:
Т₀ = (N₀ – 1) · Δt. Неопределённость возникает на границах. Прежде всего необходимо математически точно задать исходный сигнал. В данном случае его можно представить с помощью знаковой функции Sign t или с помощью функции единичного скачка h(t) (её ещё называют функцией Хевисайда):

(50а)

S(t) = 0,5∙[Sign (t) + Sign (T₀ – t)],

S(t) = h(t) – h (t – T₀).