Z-преобразование и генерация элементарных

дискретных сигналов

В данной работе изучаются основные свойства Z-преобразования и применение этого аппарата при построении схем генерации элементарных сигналов. Работа включает теоретический анализ, расчетную часть и компьютерный эксперимент по моделированию дискретных сигналов и систем.

расчетное задание

Исходные модели сигналов заданы в трех видах (рядов, рекуррентных последовательностей и непрерывных функций времени):

S₀, k = 0 (1) N₀–1,

S₁(k) =

0, k < 0, k ³ N₀;

S₀ а^к, k = 0 (1) N₀–1,

S₂(k) =

0, k < 0, k ³ N₀;

a₁ S₃(k-1) + a₂S₃(k-2), k = 0 (1) N₀–1,

S₃(k) =

0, k < 0, k ³ N₀;

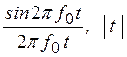S₀ £ Т,

S₄(t) =

0, çt ç > T;

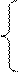S₀ сos (2p f₀ t - j₀), t Î [0, T],

S₅(t) =

0, t Ï [0, T].

При подготовке к компьютерному эксперименту предварительно необходимо уточнить дискретную модель сигнала и значения его параметров, определить Z-преобразования, составить соответствующие схемы и алгоритмы генерации, выполнить контрольные проверки.

1. Для модели S₁(к) с параметрами S₀ = 10 и N₀ (задается по варианту: N₀ = 6, 8, 10, 12) предварительно выполните следующее:

- определите Z-преобразование D₁(z)-сигнала и представьте его в двух формах;

- для контроля путем обращения Z-преобразования вычислите значения S₁(0) и S₁(1);

- составьте нерекурсивную и рекурсивную схемы генераторов, запишите алгоритмы их функционирования;

- для контроля по алгоритмам определите значения S₁(0), …, S₁(N₀–1), результаты представьте графиком.

2. Для модели S₂(к) с параметрами S₀ = 10, N₀ = 5, а= е^-a (здесь a задается по варианту: a= 0,1; 0,2; 0,3; 0,4) предварительно выполните ту же последовательность операций, что и для S₁(к).

3. Для рекуррентной последовательности S₃(k) (анализ см.в прил. 1) с параметрами N₀ =11, a₁ и a₂ (они задаются вариантом: (a₁, a₂) = (2, -1); (0, -1); (1, -1); (2, -2)) предварительно выполните следующее:

- составьте всю последовательность S₃(0), …, S₃(N₀–1) и запишите полный алгоритм ее формирования;

- определите Z-преобразование D₃(z);

- для контроля путем обращения Z-преобразования вычислите значения S₃(0) и S₃(1);

- составьте схему генерации с точными значениями всех параметров;

- представьте S₃(k) графиком.

4. В исходной модели S₄(t) заданы три параметра: S₀ = 10, Т=0,5 мс и частота f₀ (два варианта: f₀₁ = 1кГц, f₀₂ = 2 кГц). Эту модель представьте в дискретной форме

S₄(k)=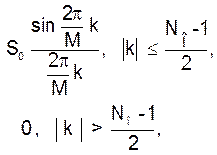

с условием: непрерывное время заменяется на дискретное t ® k D t, частота дискретизации f_Д = 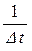= 8 кГц. Таким образом, отрезок êt ê £ T заменяется на ограничение êk ê £ 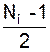с числом отсчетов N_О = 1+ 2Т f_Д = 9. Параметр М определяется отношением: М = 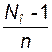, n = 2Т f₀.

Для последующего моделирования представьте S₄(k) смещенной копией S₀(k) = S₄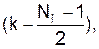

см. (24), запишите Z-преобразование D₀ (z) копии, составьте схему и алгоритм формирования копии. Изобразите графиками (с численными значениями всех параметров) функции S₄(t), S₄(k) и S₀(k).

5. Модель отрезка гармонического колебания S₅(t) с параметрами:

- амплитудой S₀ = 10 В;

- частотой f₀ (по вариантам: 1, 2, 4 кГц);

- начальной фазой j₀ (по вариантам: 0, p/6, p/3, p/2);

- длительностью Т = 1 мс

представьте в дискретной форме (частота дискретизации f_Д = 16 кГц):

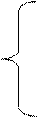S₀ cos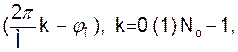

S₅(k) =

0, k < 0, k ³ N₀.

Параметры этой модели равны: N_О = f_ДТ = 16, М = 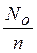, n = f₀ Т.

Перед моделированием выполните следующие процедуры:

- определите Z-преобразование D₅(z) сигнала S₅(k);

- для контроля путем обращения Z-преобразования вычислите значения S₅(0) и S₅(1);

- составьте схему генерации и алгоритм формирования сигнала S₅(k);

- для контроля по алгоритму определите первые четыре значения последовательности S₅(0), …, S₅(3);

- представьте графиками функции S₅(t) и S₅(k) с численными значениями всех параметров.

лабораторное задание

Работа выполняется на компьютере с применением пакета Matlab и его приложения Simulink. Ознакомьтесь с краткой инструкцией и демонстрационными примерами (прил. 2).

Пункты лабораторного задания выполняются в той же последователь-
ности, что и в расчетной части.

1. Используя приложение Simulink, составьте рекурсивную схему генерации сигнала S₁(k). Схема запускается единичным отсчетом (символом Кронекера). Результат работы схемы выведите на экран.

Запишите на компьютере алгоритм функционирования схемы и вычислите все значения сигнала S₁(k), к = 0 (1) N₀ =1. Пункт заканчивается сравнительным анализом всех результатов.

2. Повторите весь процесс моделирования для сигнала S₂(k). При анализе результатов обратите внимание на значение сигнала S₂(k) на такте k = N₀.

3. Выполните все аналогично для сигнала S₃(k). В данном пункте обратите внимание на следующее:

- время счета (как по схеме, так и по уравнению);

- точное обнуление схемы на тактах k = N₀, N₀ + 1, ….

Если обнуление не происходит, значит есть ошибки в параметрах нерекурсивной части схемы.

4. Используя приложение Simulink, составьте нерекурсивную схему генерации смещенной копии S₀(k) сигнала S₄(k): S₀(k) = S₄(k ),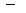
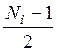k = 0 (1) N₀ , N₀= 9.

При вводе параметров b_n, n = 0 (1) N₀ схемы (b_n = S₀(n) = S₄(n –
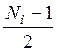– )) обратите внимание на номер n = 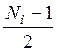(в центральной точке схемы). Значение этого параметра примите равным S₄(0) = S₀.

Схема запускается единичным отсчетом. Результат работы схемы выведите на экран. Пункт заканчивается сравнительным анализом графиков сигнала S₄(k) в расчетной и экспериментальных частях.

5. Выполните всю процедуру компьютерного моделирования (схемы и алгоритма) для сигнала S₅(k). Обратите внимание на обнуление схемы на тактах k=N₀,N₀ +1, …. Пункт заканчивается сравнительным анализом расчета и эксперимента.

содержание отчета

Отчет по работе должен включать расчетную часть и компьютерный эксперимент в соответствии с пунктами заданий:

- исходные модели сигналов;

- Z-преобразования сигналов (вывод формул);

- схемы и алгоритмы формирования сигналов;

- результаты контрольных вычислений и сравнение с экспериментом;

- графики с пояснениями;

- выводы по результатам работы.

контрольные вопросы

1. Покажите, что формула (2а) обращения Z-преобразования следует из представления функции f (Z) = D(Z^-1) в виде ряда Маклорена. Возможно ли ее применение в случае двустороннего Z -преобразования?

2. Приведите полный вывод свойств «а», «б» и «в» Z-преобразования.

3. Определите Z-преобразование последовательности S(k) = S₀d(k –
– k₀), k = 0, 1, …, k₀ - целое число. Выполните обратное Z-преобразование и сравните с функцией S(k).

4. Какие изменения (или дополнения) необходимо внести в схему
рис. 4,б (подразд. 1.3) для генерации:

- неограниченной последовательности;

- периодической последовательности (с периодом N > N₀);

- знакопеременной последовательности с периодом 2N, N > N₀?

Приведите примеры.

5. Составьте схемы генерации сигнала S₂(k), S₀ = 10, N₀ = 5,
с параметрами: 1) а = 2; 2) а = 0,5. Приведите графики генерируемых сигналов.

6. Покажите, что формула (П 1.2), см. прил. 1, задает уравнение для рекуррентной последовательности S₃(k) с фиксированным числом отсчетов. (Указание: проверьте значения S₃(N₀), S₃(N₀ + 1), …).

7. Какие изменения (или дополнения) необходимо внести в схему генерации сигнала S₄(k), если исходная модель S₄(t) (с частотой f₀ = 2 кГц) подвергается дискретизации с f_Д = 16 кГц?

8. Укажите элементы схемы генератора сигнала S₅(k), которые задают: длительность реализации сигнала, частоту, начальную фазу, амплитуду.

9. Составьте схему генерации сигнала 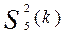. (Указание: начните с тригонометрических формул и Z-преобразования).

10. Каким образом может проявиться усеченное задание параметров (b₀, b₁, и a₁, см. рис.6 в подразд. 1.3) в схеме генерации сигнала S₅(k)? Покажите на примере.