Здесь по определению

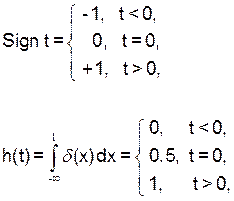
где d(x) – d-функция Дирака.

В обоих случаях (50а) имеем: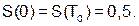

Теперь сигнал, а следовательно, и его модель S(k) = S(k∙Dt) заданы точно на всём отрезке T₀ (рис.17). Видно, что на концах импульса отсчёты в дискретной модели равны по 0,5.

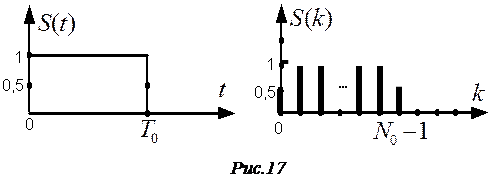Найдём z-преобразование дискретной модели сигнала. Здесь две геометрические прогрессии:

S(k) = 0,5∙[S₁(k) + S₂(k) ],

S₁(k) = 1, k = 0 (1) N₀–1, (51)

S₂(k) = 1, k = 1 (1) N₀–2.

После несложных выкладок получим:

(52)

Таким образом, модель S(k) можно представить как свёртку двух равномерных последовательностей с N₁ = N₀ – 1 ≥ 2 и N₂= 2 отсчётами. Соответствующая схема генератора дискретной модели сигнала S(k) показана на рис.18.

Рис.18

В заключение отметим, что операция свёртки является одной из основных процедур в системах цифровой обработки сигналов. Главная проблема в таких системах – решение задач в режиме реального времени. Прямые методы вычисления сверток по (45), (45а) или соответствующие схемы ЛПП-систем могут включать большое количество операций умножения. Именно они снижают скорость вычислений. В теории дискретных систем для задач цифровой обработки сигналов разработан ряд эффективных методов и алгоритмов «быстрой» свёртки. Эти методы будут рассматриваться в других работах.

1.7. Эффекты квантования в схемах генерации

Выше рассматривались идеализированные схемы генерации, построенные в точном соответствии с z-преобразованием дискретного прототипа сигнала. Однако в реальных схемах учитывается ряд технических ограничений.

Прежде всего, как отмечалось, параметры (коэффициенты а_i и b_i) и результаты арифметических операций (сложения, умножения) в схеме должны записываться в виде кодов. Это накладывает определенные ограничения на точность представления параметров и переменных. В итоге схема восстанавливает сигнал с ошибкой:

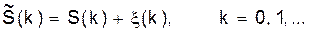. (53)

Эту ошибку ξ(k) называют шумом квантования.

При проектировании ЛПП-системы источник такого специфического “шума” представляют некоторым эквивалентным генератором (рис. 19).

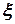(k)

Рис. 19

Характеристики «шума» ξ(k) зависят от вида схемы (формы построения) и способа задания параметров.

Применительно к схеме генератора ошибку ξ(k) можно условно назвать шумом. Точнее, ξ(k) – это погрешность аппроксимации отсчета импульсной характеристики ЛПП-системы, используемой в качестве генератора. Задача заключается в выборе такой разрядности представляемых чисел (следовательно, выборе числа позиций в кодах), чтобы результирующая погрешность восстановления сигнала не выходила за рамки допустимых значений. В качестве такой меры при восстановлении сигнала S(k), k = 0 (1) N₀–1, можно использовать, например, следующее ограничение:

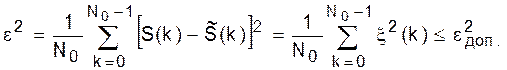(54)

Наиболее простой и естественный ввод ограничений на точность представления параметров и переменных – это запись их в усеченном виде. Усечение выполняется путем отбрасывания младших разрядов числа. Эта процедура должна быть одинаковой на всех этапах генерации сигнала и такой, чтобы все числа укладывались в общую и ограниченную разрядную сетку.

Примечание. При кодировании и записи чисел в цифровых устройствах используют два формата: с «фиксированной запятой» и c «плавающей запятой». Кратко отметим особенности этих форматов [2, 5, 6]. Они соответствуют двум формам представления числа X:

(55)

В первом варианте фиксируется количество разрядов (обычно двоичных) в целой E(X) и дробной e(X) частях. Например, десятичное число 1,375 можно записать в формате с фиксированной («двоичной») запятой, выделив два разряда на целую часть и три – на дробную: 01,011. Этот формат образуется путем усечения числа X (с округлением или без округления сохраняемого разряда), имеет ограниченный диапазон чисел, прост в реализации и обеспечивает высокое быстродействие схемы. Формат с плавающей запятой задается порядком числа m(X) (как целое со знаком) с основанием обычно а = 2 и мантиссой b(X) (как дробное число с фиксированной запятой). Этот формат благодаря знаку порядка m(X) может охватывать большой диапазон чисел и обеспечивать высокую точность их представления. Однако он сложен в реализации (при сложении и умножении чисел).

Здесь для простоты ограничимся десятичной системой с фиксированной запятой, уделяя основное внимание алгоритмам генерации и эффектам при усечении чисел.

Положим, что все константы и переменные в схеме генерации можно представить в усечённом виде с N₁+1 разрядами в целой части E(X) и только N₂ разряда (N₂ ≥ 1) – в дробной части e(X):

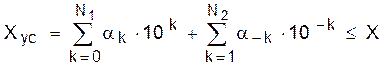. (56)

Здесь X – истинное значение; X_ус – усеченное значение как n-разрядное число (n = N₁ + N₂ + 1); α_{± k} – разрядные коэффициенты числа X (0 ≤ α_±k≤
≤ 9); α _{–N 2} – сохраняемый (значащий) разрядный коэффициент числа X. Заметим, что если α _{–N 2} представлен округленно (с учетом значений отбрасываемых младших разрядов), то запись (56) надо видоизменить: X_0k X.

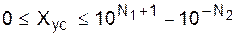Диапазон значений чисел X_ус по (56) ограничен:

. (57)

Именно в этот (общий) диапазон и должны укладываться все числа, генерируемые схемой.

Процедуру усечения можно реализовать с помощью оператора выделения целой части E(∙) числа. Есть два варианта.

1. Перепишем (56) с учетом общего (масштабного) множителя:

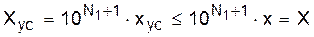. (58)

Здесь все числа x_ус являются дробными с тем же количеством разрядов
n = N₁ + N₂ + 1:

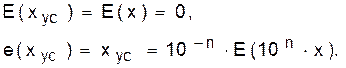(58а)

Последнюю запись можно рассматривать как алгоритм усечения дробных чисел. При этом диапазон значений усеченных чисел составляет

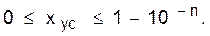(59)

2. Выберем масштабный множитель в (56) таким образом, чтобы при усечении устранялась дробная часть:

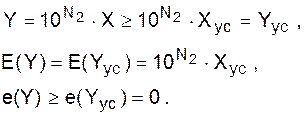(60)

Теперь все числа Y_ус являются целыми (с тем же числом разрядов n = N₁ + N₂ + 1) и укладываются в диапазон

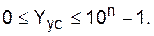(60а)

Итак, процедуру усечения можно реализовать по двум алгоритмам:

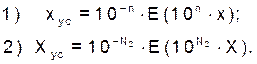(61)

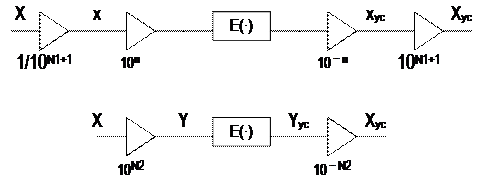
Cхематически первый и второй варианты представлены на рис. 20 а,б соответственно.

а

б

Рис. 20

Обратим внимание на масштабные множители в этих схемах. Значения их можно получить только после предварительной оценки всех возможных значений переменных в схемах генерации и учета допустимых погрешностей. (Это – характерная деталь при использовании формата с фиксированной запятой!)

Для последующего анализа схем (см. рис. 20) сделаем некоторые замечания.

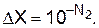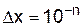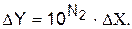Процедура усечения фактически предполагает введение равномерной дискретной (квантованной!) шкалы для всех вычислений – подобно использованию значений только на рисках мерной линейки. Шаг квантования на такой шкале задается минимальным значащим числом. Оно уже заложено в определении (56) усеченного числа: Для других вариантов усечения – по (58) и (60) – соответственно имеем: и Заметим, во всех этих случаях число уровней квантования одно и то же:

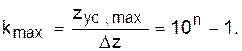(62)

Оно определяет размер шкалы.

Рассмотрим пример. Положим в (56) N₁ = 1, N₂ = 2, n = 4. Тогда для диапазона чисел и шага квантования получим:

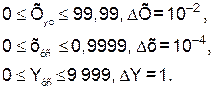
Вернемся к схеме рис.20. Функциональный элемент E(∙) назовем квантователем. Он входит в состав всех схем аналого-цифрового преобразования (АЦП) [6].

Модель квантователя составим следующим образом. Представим целую и дробную части числа X ≥ 0 в виде

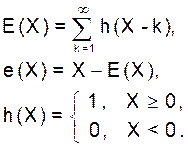(63)

Здесь h(X) – функция единичного скачка (или функция Хевисайда), а E(X) – фактически счетчик этих функций. Заметим, что точность представления функции h(X) (cм. ее запись в (50а)) не влияет на определение E(X).

Выражение E(X) в (63) можно рассматривать как оператор усечения дробной части числа, а e(X) – как погрешность при усечении. Эти функции показаны на рис.21.

Рис.21

График E(X) называется характеристикой квантователя с усечением. В данном случае шаг квантования Δ равен единице. Число уровней квантования k_max (как верхнее значение индекса k в сумме (63)) определяется верхней границей числа X. Так, для записи (56) имеем:

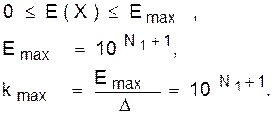
Параметры квантователей по схемам (см. рис.20) фактически уже определены. Так, в первом варианте (см. рис.20,а) получим:

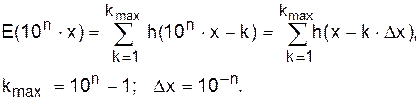(64)

Аналогично по схеме, приведенной на рис. 20,б, имеем:

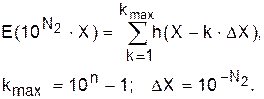(65)

Итак, квантование в первой схеме выполняется по алгоритму (64), шкала уровней (значений x_ус) будет дискретной с шагом 10 ^–n (см. множитель в схеме на рис.20,а). Во второй схеме (см. рис. 20,б) всё аналогично с той лишь разницей, что шкала уровней имеет шаг 10 ^{–N 2}.

Примечания. 1. Характеристики двустороннего квантователя (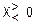) представляются следующим образом. Для вещественных X выделяют две компоненты – абсолютное значение и знак: X = |X|∙Sign X. Теперь вместо (63) имеем:

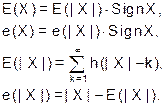(66)

Функции E(X) и e(X) показаны на рис.21 пунктиром.

2. В случае процедуры усечения с округлением характеристики квантователей (одностороннего и двустороннего) смещены:

(67)

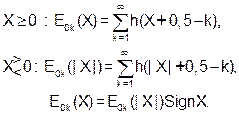Указанные схемы и алгоритмы позволяют создавать имитационные модели генераторов и исследовать специфические эффекты квантования в реальных системах.

Примечание. В реальных схемах усечение выполняется автоматически. Достаточно лишь выбрать, как отмечалось, определенную разрядную сетку для представления всех чисел и необходимое количество разрядов в сумматорах и регистрах памяти. При этом важно исключить две ситуации: переполнения и обнуления. Эффект переполнения возникает при сложении и умножении чисел, когда результат выходит за верхнюю границу общего диапазона чисел (для (56) это X > 10 ^{N 1 +1} ). Эффект обнуления имеет место при умножении дробных (меньших единицы) чисел, когда результат оказывается меньше наименьшего значащего числа (для (56) это
X < ∆X = 10 ^{–N 2}).

Анализ проведем на примере имитационной модели генератора убывающей последовательности (17) с параметрами: a = e ^–α, α > 0, S₀ = 1:

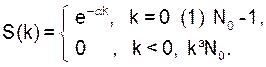(68)

В данном случае усечению подлежат единственный параметр a < 1 и его степени a ^k, k ≤ N₀, см. (18). Положим, что при усечении необходимо сохранить n разрядов (после запятой). Это можно реализовать по схеме усечения дробных чисел (см. рис. 20,а) с параметрами квантователя: ∆x = ∆a = = 10 ^–n и k_max=10 ⁿ –1. Масштабирующий множитель 1/10 ^{N 1 +1} в схеме исключается (он необходим только в случае S₀ > 1).

На рис.22 представлены эквивалентная схема (a) и имитационная модель (б) генератора в нерекурсивном варианте.

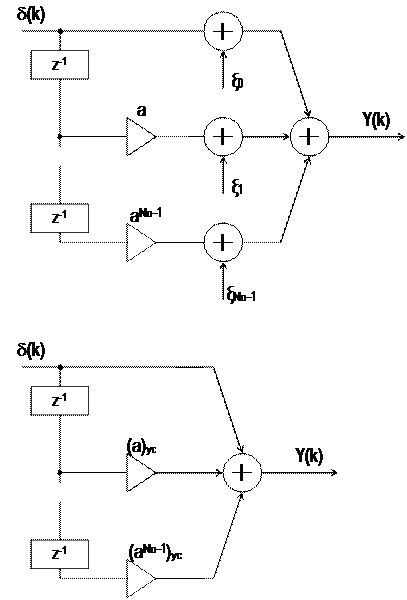а

б

Рис.22

В эквивалентной схеме показаны источники ошибок, вносимых при усечении параметров:

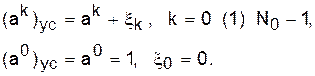(69)

Схема на рис. 22,б восстанавливает сигнал 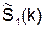по алгоритму

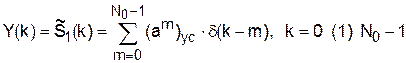. (70)

В данном варианте генератора можно обойтись без квантователя – подготовленные усечённые значения параметров вводятся в схему непосредственно.

Результирующую погрешность (54) при восстановлении сигнала оценим следующим образом. В процессе усечения чисел a^k по первому правилу в (61) образуются остатки ε_k, k = 0 (1) N₀–1:

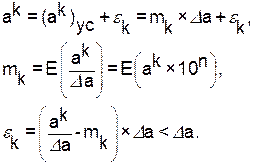(71)

Примечание. Формально и при моделировании уровень квантования m_N в соответствии с (63) записывается в виде

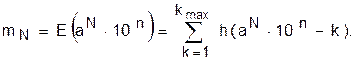
Эти остатки и составляют вносимую погрешность:

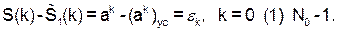
Итак, результирующая погрешность (54) равна

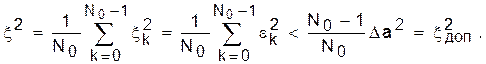(72)

В рекурсивном варианте эквивалентная схема и имитационная модель генератора убывающей последовательности (68) принимают вид, представленный на рис. 23,а,б соответственно (сравните с рис.5).

Как и выше, в имитационную модель усечённые значения параметров –(a^No)_yc и (a)_yc вводятся непосредственно. Параметр (а)_ус перед квантователем Е(∙) объединён с множителем 10 ⁿ.

а

б

Рис.23

Обратите внимание на то, что в эквивалентной схеме указаны всего два источника ошибок. Но источник ξ_a(k) символизирует все ошибки, которые образуются при усечении многократных произведений по кольцу обратной связи, включая и ошибку при усечении параметра а. (В таких ситуациях говорят, что ошибка накапливается или размножается.)

Имитационная модель (см. рис.23,б) функционирует по алгоритму (сравните с (19))

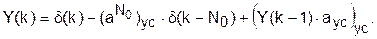(73)

Здесь, в соответствии с правилами усечения (71),

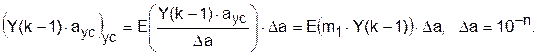(74)

В частности, из алгоритма (73) следует:

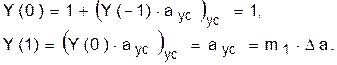
Первая строчка записана с учётом определения: Y(–1) = 0.

Схема рис.23,б восстанавливает отсчёты искажённого сигнала 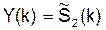(который отличается от 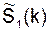). Из (73) и (74) следует рекуррентная формула для генерируемого сигнала:

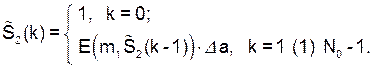(75)

Заметим, что в отличие от идеализированной схемы рис.5 здесь на такте k = = N₀ может не произойти обнуления (см. второе слагаемое в (73)):

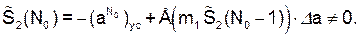(76)

Как следствие, схема будет генерировать некоторую остаточную последовательность отсчётов (по той же рекуррентной формуле (75)) за границами заданного интервала k = 0 (1) N₀–1. Это является одним из основных недостатков рекурсивных схем с усечением параметров.

Примечание. Остаточные явления могут проявляться в так называемых «межсимвольных» искажениях [4].

Оценим погрешность, которую даёт схема рис.23,б (в сравнении с идеализированной схемой рис.5) при генерации сигнала на заданном интервале k = = 0 (1) N₀–1. Ошибка на каждом такте равна:

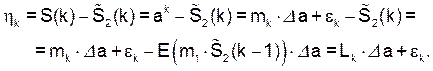(77)

Здесь 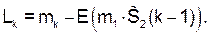. (77а)

В этих записях учтены обозначения в (71) и (75). Как и в нерекурсивном варианте, можно заметить, что η₀ = 0, η₁ = ε₁ (так как L₁ = 0). Теперь для результирующей погрешности имеем:

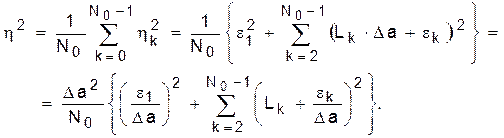(78)

Учитывая, что остатки ε_k < Δa для всех k (см. (71)), окончательно получим оценку

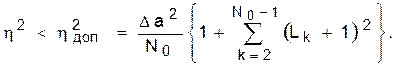(79)

Сравним две имитационные модели рис.22,б и 23,б при генерации сигнала (68) с параметрами: a = e ^–α, α = 0,2, N₀ = 5. При усечении сохраняем два разряда после запятой n = 2, при этом шаг квантования составит
Δa = 10^–2.

Прямые расчёты среднеквадратической погрешности по (72) дают:

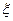² ≈ 3.3∙10^–5; 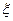²_доп = 8∙10^–5.

В рекурсивном варианте по (78) и (79) соответственно получим (L₂ = 2, L₃ =
= 2, L₄ = 7): η² ≈ 1,34∙10^–3; η²_доп = 1,66∙10^–3. Дополнительно можно вычислить значение 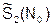по (76). Оно равно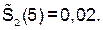

Сравнение показывает, что в рекурсивном варианте сигнал искажается больше (погрешность на два порядка выше). Точного обнуления на границе
(k = N₀) не происходит.

Обобщая этот пример, отметим, что рекурсивные схемы с квантователем дают не только большую погрешность и переходные процессы. Следствием могут быть более сложные эффекты. Так, в случае генераторов гармонических функций возможны «паразитные» амплитудная, частотная или фазовая модуляции.