[убрать]
· 1 Сложение векторов
· 2 Умножение на число
· 3 Свойства линейных операций
o 3.1 Примечание
· 4 Линейные комбинации
· 5 Смотри также
Сложение векторов[править]

Параллельный перенос
Под параллельным переносом вдоль вектора понимают перемещение всех точек пространства в одном направлении на одинаковое расстояние. Определим сложение векторов так, чтобы последовательные сдвиги вдоль двух векторов соответствовали сдвигу вдоль суммы этих векторов.
Пусть даны два вектора 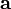 и
и 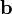 . Приложим вектор
. Приложим вектор 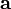 к некоторой точке
к некоторой точке  , получим
, получим 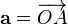 . Приложим вектор
. Приложим вектор 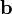 к точке
к точке 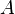 , получим
, получим 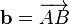 . Тогда вектор
. Тогда вектор 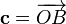 будем называть суммой векторов:
будем называть суммой векторов: 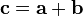 .
.
Докажем, что данное определение не зависит от выбора точки 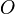 .
.
Приложим вектор 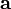 к другой точке
к другой точке 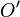 , получим
, получим 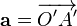 . Приложим вектор
. Приложим вектор 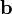 к точке
к точке 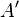 , получим
, получим 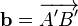 .
.
Рассмотрим направленные отрезки 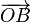 и
и 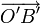 . Они, очевидно, равны (см. рис.), поскольку
. Они, очевидно, равны (см. рис.), поскольку 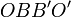 — параллелограмм.
— параллелограмм.
Умножение на число[править]
Произведением вектора 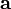 на число
на число 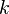 называется вектор, который:
называется вектор, который:
1. коллинеарен вектору 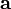 ;
;
2. сонаправлен ему, если 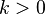 , или противоположнонаправлен, если
, или противоположнонаправлен, если 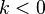 ;
;
3. длины связаны следующим соотношением: 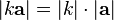 .
.
Данное определение согласовано с определением сложения:
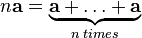
|
для любого натурального 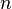 .
.
Свойства линейных операций[править]
Коммутативность сложения векторов
Ассоциативность сложения векторов
Сложение векторов коммутативно: 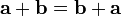 .
.
Сложение векторов ассоциативно: 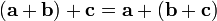 .
.
Прибавление нулевого вектора к любому не меняет последнего: 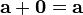 . Очевидно,
. Очевидно, 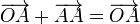 .
.
Для любого вектора 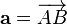 существует вектор
существует вектор 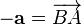 такой, что
такой, что 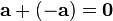 или
или 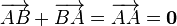 .
.
Умножение вектора на число ассоциативно: 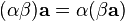 . Умножение вектора на число дистрибутивно относительно сложения чисел:
. Умножение вектора на число дистрибутивно относительно сложения чисел: 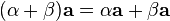 .
.
Доказательство сводится к перечислению всех возможных знаков 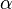 и
и 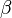 , в каждом случае утверждение очевидно.
, в каждом случае утверждение очевидно.
Дистрибутивность умножения векторов относительно сложения
Умножение вектора на число дистрибутивно относительно сложения векторов: 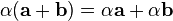 . Это следует из подобия треугольников
. Это следует из подобия треугольников 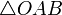 и
и 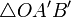 на рисунке.
на рисунке.
Очевидно, умножение на единицу не меняет вектор: 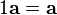 .
.
Примечание[править]
В алгебре изучаются так называемые алгебраические структуры. Это множества математических объектов, для которых определены некоторые операции, удовлетворяющие некоторым системам аксиом.
Пример такой структуры, изучаемой в линейной алгебре, — так называемое векторное (линейное) пространство. Это множество векторов, для которых определены операции сложения и умножения на элементы некоторого поля (например, поля вещественных чисел), причем эти операции удовлетворяют указанным выше свойствам.
В линейной алгебре изучаются общие свойства таких множеств, их элементы (их называют абстрактными векторами) не обязаны быть геометрическими векторами (хотя чаще всего именно их приводят в качестве наглядного примера).
В аналитической геометрии векторы нужны, в первую очередь для введения системы координат (см. ниже). Благодаря этому удается описать геометрические фигуры при помощи аналитических формул.
Линейные комбинации[править]
Линейная комбинация векторов 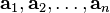 с коэффициентами
с коэффициентами 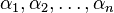 — вектор
— вектор 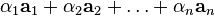 . Если все коэффициенты равны нулю, линейную комбинацию называют тривиальной, иначе — нетривиальной.
. Если все коэффициенты равны нулю, линейную комбинацию называют тривиальной, иначе — нетривиальной.
Векторы 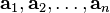 называются линейно зависимыми, если существует их нетривиальная комбинация, равная нулю.
называются линейно зависимыми, если существует их нетривиальная комбинация, равная нулю.
Теорема
Система векторов линейно зависима тогда и только тогда, когда один из векторов является линейной комбинацией остальных.
Доказательство [скрыть]
Необходимость. Пусть система векторов линейно зависима. Это значит, что существует нетривиальная линейная комбинация, равная нулю: 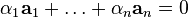 . Один из коэффициентов, например . Один из коэффициентов, например 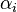 не равен нулю. Тогда не равен нулю. Тогда
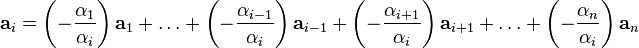 Достаточность. Пусть
Достаточность. Пусть 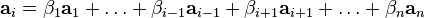 . Тогда . Тогда
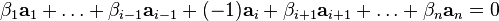 Это нетривиальная (коэффициент
Это нетривиальная (коэффициент 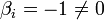 ) линейная комбинация, равная нулю. Значит система векторов линейно зависима. ) линейная комбинация, равная нулю. Значит система векторов линейно зависима.
|
 2015-01-30
2015-01-30 978
978








