Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы)

Пусть система линейных алгебраических уравнений задана в матричной форме 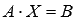, где матрица A имеет размерность n на n и ее определитель отличен от нуля.

Так как 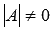, то матрица А – обратима, то есть, существует обратная матрица 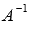. Если умножить обе части равенств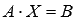а на 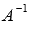слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных . Так мы получили решение системы линейных алгебраических уравнений матричным методом.

Пример.

Решите систему линейных уравнений 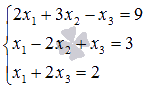матричным методом.

Решение.

Перепишем систему уравнений в матричной форме:

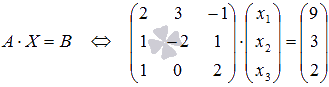
Так как

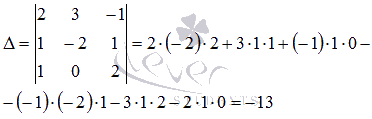
то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как .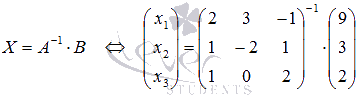

Построим обратную матрицу 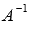с помощью матрицы из алгебраических дополнений элементов матрицы А (при необходимости смотрите статью методы нахождения обратной матрицы):

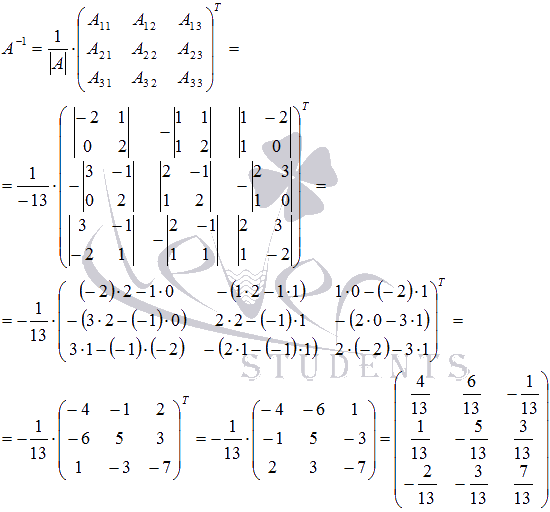
Осталось вычислить 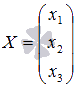- матрицу неизвестных переменных, умножив обратную матрицу 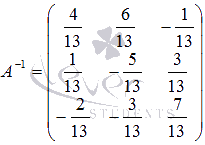на матрицу-столбец свободных членов 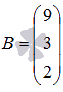(при необходимости смотрите статью операции над матрицами):

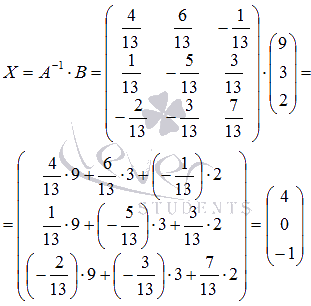
Ответ:

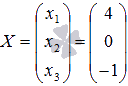или в другой записи x₁ = 4, x₂ = 0, x₃ = -1.

Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.

Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.

К началу страницы