Задача № 3

Провести полное исследование функции и построить график.

1. Область определения: (х - с)² - 3 ¹ 0; (х - с)² ¹ 3; х - с ¹ ± Ö3.

Следовательно, .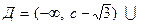

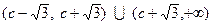2. Точки пересечения с осями:

а) ось ОУ: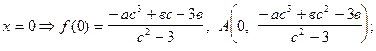

б) ось ОХ: y = 0 .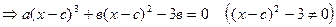

Поскольку решение кубического уравнения с параметрами выходит за пределы курса, то находить точки пересечения с осью ОХ не будем.

3. Четность, нечетность функции:

Рассмотрим 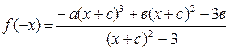и убедимся, что 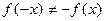, функция не является нечетной, и 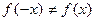- функция не является четной.

4. Функция не является периодической.

5. Монотонность, экстремальные точки:

Находим производную: .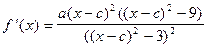

Приравниваем производную к нулю: .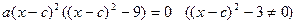

Отсюда находим три решения: х₁ = с - 3, х₂ = с, х₃ = с + 3.

Составляем таблицу:

х	f¢(x)	f(x)
(-¥, c - 3)	+	ì
c - 3	0		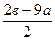Точка максимума
(c - 3, c - √3)	-	î
c - √3	Не определена	Не определена
(c - √3, c)	-	î
c	0	в
(c, c + √3)	-	î
c + √3	Не определена	Не определена
(c + √3, c + 3)	-	î
c + 3	0		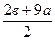Точка минимума
(c + 3, +¥)	+	ì

6. Точки перегиба. Выпуклость, вогнутость функции.

Находим вторую производную: .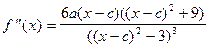

Приравниваем ее к нулю: 6а(х - с)((х - с)² + 9)=0; ((х - с)² - 3)³ ¹ 0.

Получаем единственное решение х = с и составляем таблицу:

х	f¢(x)	f(x)
(-¥, c - √ 3)	-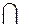
c - √3	Не определена	Не определена
(c - √3, c)	+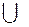
c	0	в	Точка перегиба
(c, c + √3)	-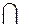
c + √3	Не определена	Не определена
(c + √3,+¥)	+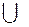

7. Асимптоты.

Вертикальные.

Поскольку знаменатель обращается в нуль при х = c - √3 и х = c + √3, а числитель нет, то вертикальные прямые х = c - √3 и х = c + √3 - вертикальные асимптоты.

Наклонные.

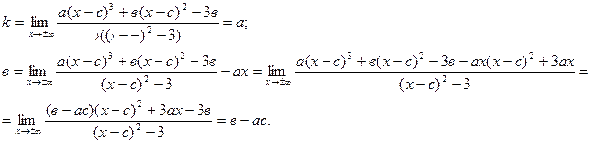Отсюда, прямая у = ах + (в - ас) - наклонная асимптота.