2015-01-30
599
План:
1. Изучение понятие локального и условного экстремумов.
2. Формулирование необходимых и достаточных условий экстремума.
3. Решение задач.
Контрольные вопросы и задачи
1)Найти стационарные точки функции
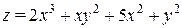
Находим частные производные первого порядка, приравниваем их к нулю и записываем систему уравнений:
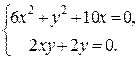
Из второго уравнения следует, что 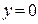или 
, или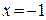 
. Подставляя по очереди эти значения в первое уравнение, найдём четыре стационарные точки:
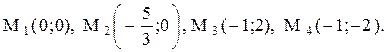
2) Ранее в примере 1 было установлено, что функция
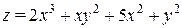
имеет четыре стационарные точки:
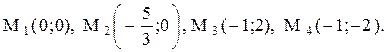
Вторые частные производные данной функции равны
.
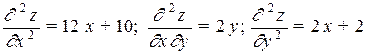В точке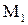 
имеем: A= 10, B= 0, C= 2. Здесь 
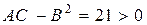, значит, точка 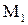является точкой экстремума, и так как A положительно, то этот экстремум – минимум. В точке 
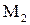соответственно будет A=– 10, B= 0, C=– 4/3. Это точка максимума. Точк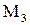и 
и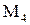 
не являются экстремумами функции, так как в них 
.
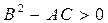3) Исследовать функции на экстремум:
1. 
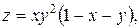
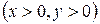. Ответ: 
.
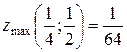2. 
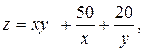
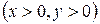. Ответ: 
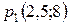– седловая точка.
3. 
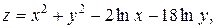
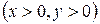. Ответ: 
.
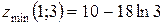4. 
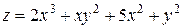. Ответ: 
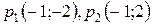– седловые точки.
4) Найти условный экстремум функции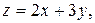 
при условии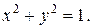 
Решение: Составим функцию Лагранжа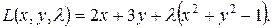 
Имеем
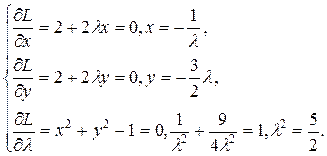
Система имеет два решения
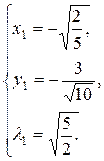
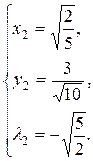
Далее,
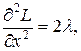
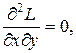
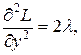
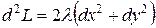
При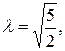 
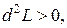поэтому функция 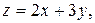в точке 
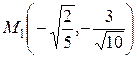имеет условный минимум, а при,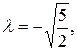 
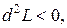следовательно, функция 
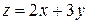имеет в точке 
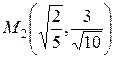условный максимум.
5)Найти условные экстремумы функции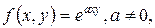 
при наличии ограничения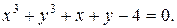 
Решение: Построим функцию Лагранжа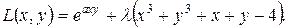 
Стационарные точки определим из системы
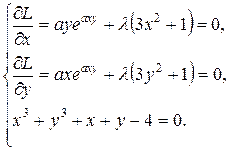
Умножим первое уравнение на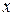 
, а второе – на 
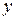. После вычитания получим
.
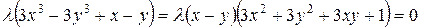Если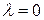 
, то из первых двух уравнений системы 
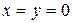. Но такие значения переменных 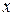и 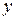не удовлетворяют уравнению связи. Значит 
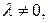и так как 
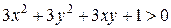, то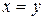 
. Подставляя это в уравнение связи, получаем: 
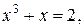откуда 
, 
.
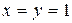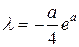Итак, единственная стационарная точка функции Лагранжа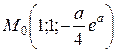 
.
Далее,
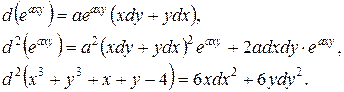
Тогда для 
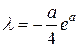при 
и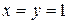 
получаем
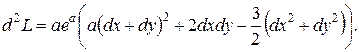
Из уравнения связи при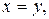 
находим соотношение для дифференциалов 
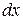и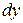 
, 
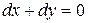, то есть 
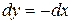. Тогда 
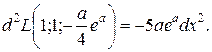Поэтому при 
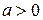в точке 
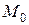функция имеет условный максимум, а при 
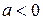– условный минимум. Экстремальное значение равно 
.
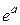Литература
Основная:
1. Высшая математика для экономистов / под ред. Н.Ш. Кремера. - М.: ЮНИТИ, 2002. С. 217–224.
2. Замков, О.О. Математические методы в экономике: учебник. / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемых. - М.:, Изд-во МГУ им. М.В. Ломоносова «ДИС», 1988. - С. 61–64, 70.
3. Ильин, В.А., Высшая математика: учебник / В.А. Ильин, А.В. Куркина. - М.: Проспект, 2009. - С. 258–258.
4. Красс, Математика для экономических специальностей: учебник / М.С. Красс. - М.: ИНФРА-М, 1999. - С. 115–117.
Дополнительная:
1. Баврин, И.И. Математика для гуманитариев: учебник / И.И. Баврин. - М.: Академия, 2011. - С. 101–111.
2. Кремер, Н.Ш. Математика для экономистов: от Арифметики до Эконометрики: учебно-справочное пособие. / Н.Ш. Кремер. - М.: Юрайт, 2011. - С. 187-198.
3. Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика.: учебно-методическое пособие / Под ред. А.Н. Данчула. - М.: РАГС, 2004. - С. 20–23.
