Практическое занятие 1 по теме: «Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке»

План:

1. Изучение понятие наибольшего и наименьшего значения функции на отрезке

2. Знакомство с алгоритмом вычисления наибольшего и наименьшего значения функции на отрезке.

3. Применение изученного алгоритма при решении задач.

Контрольные вопросы и задачи

1) Найти наибольшее и наименьшее значения функции f (x) = 2 x ³ – 6 x + 5 на отрезке .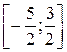

Решение. Находим критические точки, принадлежащие :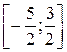

f¢ (x) = 6 x ² – 6 = 6(x ² – 1), 6(x ² – 1) = 0, x ₁ = –1, x ₂ = 1.

Вычислим значения функции в этих точках:

f (–1) = 2 × (–1)³ – 6 × (–1) + 5 = 9; f (1) = 2 × 1³ – 6 × 1 + 5 = 1.

Вычислим значения функции на концах отрезка:

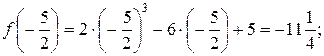
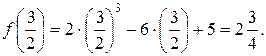
Таким образом, наибольшее значение данной функции на рассматриваемом отрезке есть f (–1) = 9, а наименьшее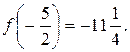

Ответ: f (–1) = 9,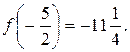

2) Найти наибольшее и наименьшее значения функции f (x) = 5 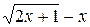на отрезке [4; 40].

Решение. Находим критические точки функции, лежащие внутри данного отрезка:

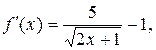
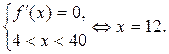
Вычисляем значения функции на концах отрезка и в критической точке: f (4) = 11, f (12) = 13, f (40) = 5. Из полученных значений выбираем наибольшее и наименьшее:

, .

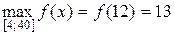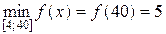Ответ: , .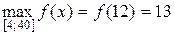

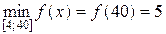3) Дана функция f (x) = | x ² – 6 x + 5 |. Найти наибольшее и наименьшее значения функции f на отрезке [2; 6].

Решение. Рассмотрим функцию f на отрезке [2; 6]:

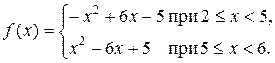
Для нахождения критических точек функции f, непрерывной на [2; 6], нужно найти внутренние точки отрезка [2; 6], в которых производная равна нулю или не существует. Имеем:

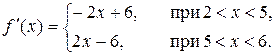
В точке x = 5 производная не существует; 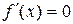при x = 3. Итак, критические точки: 3 и 5.

Вычисляем значение функции в критических точках и на концах отрезка: f (2) = 3, f (3) = 4, f (5) = 0, f (6) = 5;

, .

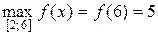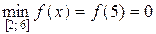Ответ: , .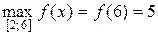

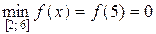4) Найти наибольшее значение функции f (x) = x ln 5 – x ln x на отрезке .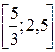

Решение. 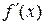= ln 5 – ln x – 1 =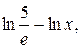 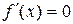при 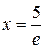. Сравнение значений функции на концах отрезка и в критической точке приводит к сложным вычислениям. Вместо этого проведем исследование функции на монотонность. Учитывая непрерывность функции в точке 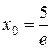и тот факт, что при 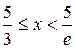производная положительна, а при 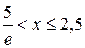отрицательна, приходим к выводу, что на промежутке 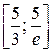функция возрастает, а на промежутке 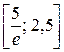убывает. Это и означает, что значение функции в точке 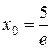является наибольшим из всех значений функции на данном отрезке.

Литература

Основная:

1. Высшая математика для экономистов / под ред. Н.Ш. Кремера. - М.: ЮНИТИ, 2002. - С. 217-224.

2. Замков, О.О. Математические методы в экономике: учебник. / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемых. - М.:, Изд-во МГУ им. М.В.Ломоносова «ДИС», 1988. - С. 61–64, 70.

3. Ильин, В.А., Высшая математика: учебник / В.А. Ильин, А.В. Куркина. - М.: Проспект, 2009. - С. 258–258.

4. Красс, Математика для экономических специальностей: учебник / М.С. Красс. - М.: ИНФРА-М, 1999. - С. 115–117.

Дополнительная:

1. Баврин, И.И. Математика для гуманитариев: учебник / И.И. Баврин. - М.: Академия, 2011. - С. 101–111.

2. Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика.: учебно-методическое пособие / Под ред. А.Н. Данчула. - М.: 2004. - С. 20–23.

3. Шипачёв В.С. Высшая математика. Базовый курс: учебное пособие / под ред. А.Н. Тихонова. - М.: Юрайт, 2011. - С. 288-293.