Приращения координат: 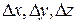 .
.
Вектор перемещения: 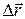 .
.
Связь между ними: 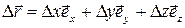
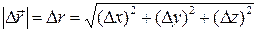
3). Характеристики быстроты изменения положения:
Вектор средней скорости (за время 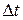 ):
): 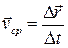 .
.
Модуль средней скорости 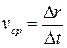 .
. 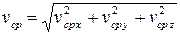 .
.
Лежит на отрезке, соединяющем начальную и конечную точки на траектории.
Проекции вектора средней скорости на оси координат: 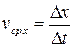 ,
, 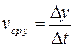 ,
, 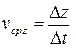
Вектор мгновенной скорости: 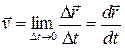
Направление вектора - по касательной к траектории.
Проекции этого вектора на оси координат: 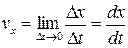 ,
, 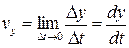 ,
, 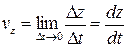 .
.
4). Характеристики неравномерности движения (быстроты изменения скорости):
Вектор ускорения: 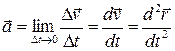
Проекции этого вектора на оси координат: 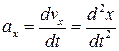 ,
, 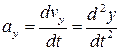
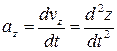
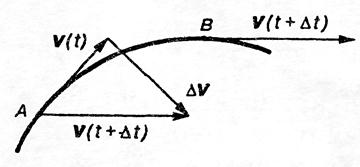 Рис. 2.
Вектор ускорения направлен туда же, куда и вектор изменения скорости. Они могут быть направлены куда угодно. Это определяется взаимодействиями тела с другими телами.
Рис. 2.
Вектор ускорения направлен туда же, куда и вектор изменения скорости. Они могут быть направлены куда угодно. Это определяется взаимодействиями тела с другими телами.
| 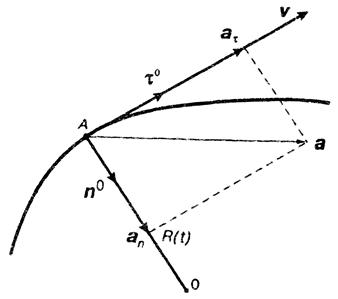 Рис. 3. Рис. 3.
|
| В каждый момент движения вектор ускорения можно разложить на две составляющих, направленных: 1) вдоль касательной к траектории (тангенциальное ускорение) 2) перпендикулярно ей (нормальное ускорение). |
| Тангенциальное ускорение | Нормальное ускорение |
| математически определяется согласно выражению | математически определяется согласно выражению |
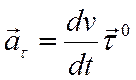
| 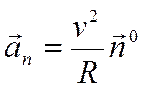 (R – радиус кривизны траектории в данной ее точке)
(R – радиус кривизны траектории в данной ее точке)
|
| Характеризует быстроту изменения модуля мгновенной скорости | Характеризует быстроту изменения направления вектора скорости |
Существует связь между этими величинами:
| Векторная форма связи | Скалярная форма связи |
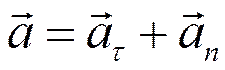
| 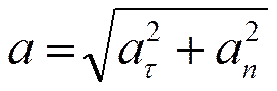
|
 2015-01-30
2015-01-30 269
269








