Поток событий

Поток событий представляет собой специфический случайный процесс, позволяющий осуществить переход от анализа микропараметров системы к анализу обобщенных характеристик ее.

Любое рассматриваемое событие может иметь несколько характеристик: момент поступления, длительность обслуживания, особенности обслуживания. Потоки таких событий называют неоднородными. Если поток характеризуется одним параметром, то его называют однородным. Нас будут интересовать однородные потоки, задаваемые законом распределения или последовательностей моментов поступления заявок, или числа заявок на заданном отрезке времени.

Для такого описания случайного процесса нужно знать многомерный закон распределения его в различные моменты времени. Таких данных практически не бывает. Приходится ограничиваться более простыми описаниями.

Таким вспомогательным процессом является так называемый простейший поток. С его помощью можно описать более сложные процессы.

Простейший поток обладает тремя свойствами:

А) стационарностью – вероятность попадания определенного числа событий на участок времени длиной t зависит только от длины участка и не зависит от положения этого участка на оси времени;

Б) ординарностью – вероятность попадания на элементарный участок Dt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события (то есть заявки приходят поодиночке, а не парами, тройками и т.д.);

В) без последействия – для любых не перекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие (т.е. заявки поступают независимо друг от друга).

Для простейших потоков вероятность того, что за время t произойдет ровно m событий, подчиняется закону Пуассона и выражается формулой

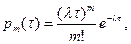(7.1)

где l - плотность распределения числа событий.

В простейшем потоке математическое ожидание числа событий и дисперсия числа событий равны величине (lt).

Второй важной характеристикой простейшего потока является закон распределения длины промежутка между соседними событиями.

Если обозначить через Т – промежуток времени между соседними событиями, то p(T< t) =F(t) - функция распределения. Вероятность противоположного события p(T ³t) =1-F(t) – есть вероятность того, что на участке времени длиной t не появится ни одного события. Она вычисляется по (4.1) при m=0 и равна величине e^-lt. Поэтому

F(t)=1- e^-lt. (7.2)

Дифференцируя, найдем искомую плотность распределения длины промежутка между соседними событиями

w(t)=l e^-lt. (7.3)

Закон этот называется показательным (или экспоненциальным) с математическим ожиданием, равным 1/l, и дисперсией равной 1/l².

Если рассматривать сумму (к+1) случайных величин, распределенных по показательному закону, то ее плотность распределения подчиняется закону Эрланга к-го порядка

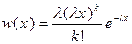, x³0. (7.4)

Математическое ожидание суммарного потока

.

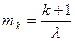Дисперсия его

.

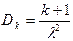Потоки Эрланга расширяют возможности анализа реальных потоков от случаев отсутствия последействия (при к=0) до жесткой функциональной связи между моментами появления событий (при к=¥).