Условия задачи отличаются от рассмотренных в разделе 4.3 тем, что здесь предусмотрена очередь для заявок, заставших все приборы обслуживания занятыми. От этого меняется число возможных состояний системы: еще добавляются состояния, определяемые, числом заявок в очереди, а очередь может быть до бесконечности. Возникает необходимость определения времени нахождения заявок в очереди, числа заявок в очереди.
Рассмотрим подробно СМО с ожиданием с одним прибором обслуживания и бесконечной очередью. Для нее диаграмма переходов из состояния в состояние показана на рис 7.5.
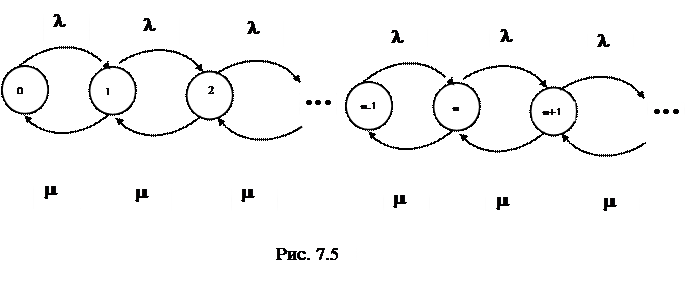 |
В этой системе интенсивность перехода «вверх» равна l, а «вниз» – равна m.
Уравнение равновесного состояния имеет вид lPn-1 = mPn.
Отсюда:
Pn=r Pn-1=… rnpo, (7.16)
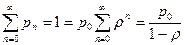 , (7.17)
, (7.17)
p0=1-r, (7.18)
pn=rn(1-r). (7.19)
Из (4.18) можно заключить, что величина r характеризует коэффициент использования прибора.
Среднее число требований в системе
N= 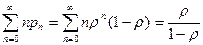 . (7.20)
. (7.20)
Существует теорема Литтла, которая утверждает, что в равновесном состоянии среднее число N требований (заявок) в системе и среднее время T нахождения заявки в системе связаны соотношением
N=lT. (7.21)
Теорема имеет широкий диапазон применений. С учетом ее, для нашего примера (4.20) получаем
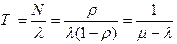 . (7.22)
. (7.22)
Среднее время нахождения заявки в очереди
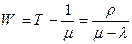 . (7.23)
. (7.23)
Среднее число заявок в очереди определяется по теореме Литтла
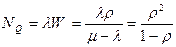 . (7.24)
. (7.24)
Если число приборов в СМО равно m, то имеем два равновесных уравнения:
lpn-1= n mpn n£ m
lpn-1= m mpn n>m.  (7.25)
(7.25)
Из них получаем
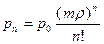 n£m
n£m
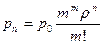 n>m
n>m  (7.26)
(7.26)
Вероятность того, что все приборы будут заняты и надо вставать в очередь, равна
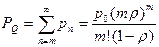 . (7.27)
. (7.27)
Среднее число заявок в очереди
NQ = 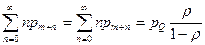 . (7.28)
. (7.28)
Отношение
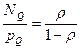 . (7.29)
. (7.29)
По теореме Литтла:
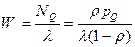 , (7.30)
, (7.30)
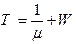 , (7.31)
, (7.31)
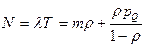 . (7.32)
. (7.32)
Вероятность встать в очередь определяется формулой
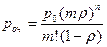 , (7.33)
, (7.33)
которая называется 2-ой формулой Эрланга.
 2015-01-30
2015-01-30 914
914








