Информационная сеть представляет собой совокупность узлов связи, соединенных между собой определенным образом каналами связи.
Сети встречаются в природе, в технических системах и используются в различных сферах деятельность человека: сеть дорог, электрические сети, водопроводные сети и т.д. Они обеспечивают экономию ресурсов, повышение живучести, объединение разрозненных ресурсов, повышение качества обслуживания распределенных в пространстве пользователей (или приборов), повышение эффективности использования обслуживающих приборов.
Сложились методы анализа и синтеза сетей различного назначения, а также основы теории сетей вообще. Однако без учета специфики информационных сетей невозможно в полной мере использовать мере использовать методы из других сфер деятельности.
Особенности информационных сетей заключаются в следующем:
1. Они предоставляют услуги своим абонентам не одного вида, как это делается в электрических, водопроводных или газовых сетях, а многих видов: передача, обработка, хранение, документирование, отображение и т.д.
2. Приборы обслуживания находятся как в узлах сети (центры обработки, хранения и т.д.), так и в ветвях (каналы связи). Все они являются элементами коллективного использования.
3. Методы обслуживания абонентов разнообразные: от предоставления приборов сети в кратковременную аренду до выполнения по их заказам определенных преобразований информации.
4. пользователи (абоненты) сети конкурируют друг с другом в различные моменты времени за право использования услуг.
5. Пользователи и приборы обслуживания распределены в пространстве.
6. Случайный характер возникновения потребностей в обслуживании у абонентов.
Все эти особенности необходимо учитывать при системном анализе информационных сетей. Кроме того, необходимо учитывать принципиальные отличия информации и сигналов, несущих информацию, как объектов преобразования в информационной сети, от материалов (веществ), являющихся объектами преобразования (обработки) в сетях другого назначения. Информацию, как образ, отражение реального объекта, можно просто и быстро многократно копировать и копия не будет хуже оригинала. Ее можно уничтожать в одном месте и просто воссоздавать в другом по некоторым признакам, если встречаются трудности по перемещению. Эти особенности информации облегчают задачи построения информационных сетей и в то же время ограничивают возможности применения результатов общей теории связи.
В ИС сеть рассматривается как элемент подсистемы распределения информации между абонентами и приборами обслуживания. Различают первичные и вторичные сети.
Первичные сети состоят из совокупности физических линий и узлов с устройствами коммутации и выделения каналов на них. Она определяет физические возможности информационной сети по организации обслуживания абонентов и характеризуется следующими параметрами:
1. Структурой (число узлов, их расположение, число ветвей, связывающих узлы).
2. Пропускной способностью (числом стандартных каналов в ветвях, типы каналов).
3. Возможностью выделения групповых трактов и отдельных каналов.
4. Надежностью и живучестью узлов и ветвей.
5. Информационной безопасностью.
6. Экономическими затратами на строительство и
эксплуатацию.
Вторичные сети создаются на базе имеющихся каналов первичной сети путем соответствующего соединения их на узлах для создания сквозных трактов от абонентов к абонентам. По способу соединения каналов на узлах вторичные сети делятся на:
· некоммутируемые;
· коммутируемые;
· с коммутацией сообщений.
В некоммутируемых сетях каналы на узлах соединения с помощью пайки или зажимов (кроссовые соединения). это долговременные соединения.
В коммутируемых сетях на узлах имеются устройства коммутации (УК) для оперативного переключения каналов.
В сетях с коммутацией сообщений на узлах, кроме УК, есть еще запоминающие устройства (ЗУ) и аппаратура, обеспечивающая прием из канала дискретной информации и выдачу ее в другой канал в соответствии с адресом (после ожидания очереди в ЗУ).
Структуры сетей могут быть различные. Различают:
Топологические структуры определенным образом унифицируются. Чаще всего используются структуры: узловые, радиальные, радиально-узловые. Узлы делятся на категории, сети разбиваются на зоны. Такое разделение обеспечивает взаимодействие международных, национальных, региональных, городских, районных сетей между собой. Узлы высоких категорий соединены каждый с каждым, а узлы более низких категорий соединены по радиально-узловому методу. Так образуется иерархия сетей.
Для повышения живучести и надежности сетей иногда используются решетчатые структуры. В них в узлах решетки организуются опорные узлы (У I) - узлы высшего ранга. К ним (к одному или двум) подключаются узлы - концентраторы (У II), к которым подходят абонентские линии.
Функциональные структуры зависят от решаемых задач, от числа и размещения абонентов и приборов, вовлеченных в процесс решения.
Предусматривается система управления сетью. Она предназначена для:
· сбора информации о состоянии элементов сети;
· определения работоспособности системы;
· принятия мер по поддержанию в допустимых пределах характеристик сети;
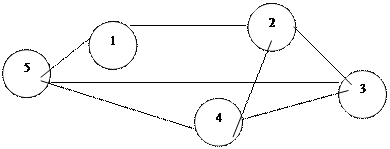
Рассмотрим метод построения дерева путей на примере сети, представленной на рис 8.2 для двух узлов: узла 2 и узла 1.
 | |||
|
Матрица связности этой сети:
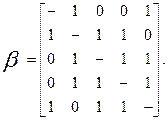
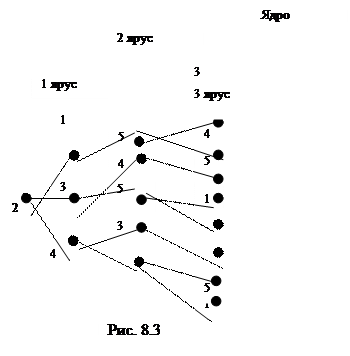
Строим дерево путей для узла 2 по рис 8.3. Для этого выписываем узел 2 и определяем узлы 1-го яруса. Это будут узлы 1,3 и 4.
 | |||
Они видны из рис. 8.2, проще пользоваться матрицей связности 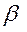 . Узлы 1-го яруса определяются по 2-ой строке этой матрицы (т.к. строится дерево путей для 2-го яруса). Учитываются те узлы, которые в матрице
. Узлы 1-го яруса определяются по 2-ой строке этой матрицы (т.к. строится дерево путей для 2-го яруса). Учитываются те узлы, которые в матрице 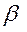 по 2-ой строке отмечены единицами. Узлы 2-го яруса находим аналогично, но с учетом, что:
по 2-ой строке отмечены единицами. Узлы 2-го яруса находим аналогично, но с учетом, что:
1) исходными являются узлы 1-го яруса (1,3 и 4) и соответственно должны будем использовать 1,3 и 4 строки матрицы 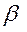 ;
;
2) исключаются узлы, для которых были образованы подмножества узлов в предыдущем ярусе (т.е. узел 2);
Тогда 2-ой ярус будет иметь узлы: 5-ый от 1-го; 4-ый и 5-ый от 3-го; 3-ий и 5-ый от 4-го узлов.
Узлы 3-го яруса находим аналогично: для 5-го – по пятой строке матрицы 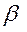 имеем «1» на 1,3 и 4. Но с 1 связь есть предыдущая. Остаются узлы 3 и 4. Для 4-го по четвертой строке имеем «1» на позициях 2,3 и 5. Для узлов 2 и 3 были уже образованы подмножества раньше. Остается узел 5. Для 5-го имеем 1,3 и 4. Но 3 было раньше. Остаются узлы 1 и 4. Для 3-го имеем единицы по третьей строке в 2,4 и 5 столбцах. Но 2 и 4 было. Остается узел 5. Наконец, для 5-го единицами отмечены позиции 1,3 и 4. Ранее было 4. Остаются узлы 1 и 3.
имеем «1» на 1,3 и 4. Но с 1 связь есть предыдущая. Остаются узлы 3 и 4. Для 4-го по четвертой строке имеем «1» на позициях 2,3 и 5. Для узлов 2 и 3 были уже образованы подмножества раньше. Остается узел 5. Для 5-го имеем 1,3 и 4. Но 3 было раньше. Остаются узлы 1 и 4. Для 3-го имеем единицы по третьей строке в 2,4 и 5 столбцах. Но 2 и 4 было. Остается узел 5. Наконец, для 5-го единицами отмечены позиции 1,3 и 4. Ранее было 4. Остаются узлы 1 и 3.
Построение дерева путей продолжается до h-го яруса, где h- максимально допустимое число переприемных участков в пути.
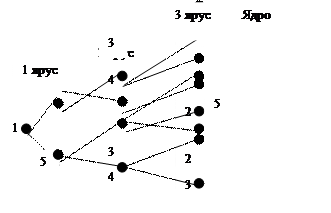
Аналогично могли бы построить дерево путей для узла 1 (см. рис. 8.4)
 | |||
|
Интерес представляет машинный алгоритм построения дерева путей для произвольного к-го узла:
1. Отмечаем узел К и выбираем к-ую строку матрицы 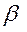 .
.
2. Выписав номера столбцов к-й строки, в которых значения элементов матрицы 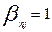 , получаем подмножество узлов 1-го яруса, образованное узлом к.
, получаем подмножество узлов 1-го яруса, образованное узлом к.
3. Образуем подмножества узлов r-го яруса (r=2,3,…,h), где h- максимально допустимое число переприемных участков пути:
а)поочередно выбираем узлы (r-1)-го яруса;
б)для каждого узла i в (r-1)-ом ярусе выбираем i-ю строку в матрице 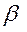 и выписываем номера столбцов с
и выписываем номера столбцов с 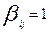 ;
;
в)исключаем номера столбцов, относительно которых были образованы подмножества узлов в предыдущих ярусах, связанных с узлом i, оставшиеся номера столбцов входят в подмножество узлов r-го яруса от узла i.
4. Построение дерева путей продолжается до h-го яруса.
По дереву путей легко проследить пути от заданного узла к другим. Перечень путей между узлами удобно записать в виде таблице путей размера k ´ m, где k – число путей, а m- число ветвей сети. Пусть, например, h £ 3 пути между узлами 2 и 5 будут (рис. 5.2)
M25={2,1,5; 2,3,5; 2,4,5; 2,3,4,5; 2,4,3,5}
Эти данные занесены в табл. 7.1. В ней каждый столбец соответствует ветви 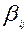 , а каждая строка – одному пути. Элемент таблицы
, а каждая строка – одному пути. Элемент таблицы 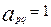 , если ветвь
, если ветвь 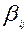 принадлежит пути
принадлежит пути 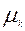 , и
, и 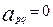 в противном случае. Для упрощения записей случаи
в противном случае. Для упрощения записей случаи 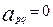 в таблицу не заносятся.
в таблицу не заносятся.
Таблица 7.1.
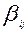 | 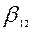 | 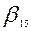 | 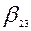 | 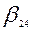 | 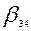 | 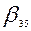 | 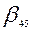 |
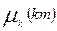 | |||||||
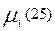 | |||||||
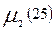 | |||||||
 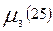 | |||||||
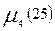 | |||||||
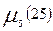 |
Оптимизационные задачи на сетях исследуются на модели выбора кратчайшего пути. Сущность этой модели проста. Задается сеть, каждой ветви которой соответствует некоторое расстояние. Нужно найти кратчайший путь в заданный узел от любого другого узла сети. Ветви могут измеряться не только единицами длины, но и стоимостью, временем, затрачиваемым на преодоление данного пути и т.д. Поэтому задача выбора кратчайшего пути имеет много приложений. Она может быть сведена к поиску пути минимальной стоимости или пути минимальной продолжительности и т.д. Эта задача в математическом смысле эквивалентна задаче о назначениях и сводится к моделям линейного программирования, сходных с задачами распределения ресурсов, выбора маршрута и т.д. Однако существуют особенности сетевых моделей, помогающие существенно повысить эффективность процесса отыскания оптимальных решений.
Общая математическая постановка задачи о кратчайшем пути:
минимизировать
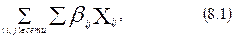
где i, j – номера узлов:
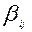 - длина (стоимость, время, живучесть и т.д.) пути;
- длина (стоимость, время, живучесть и т.д.) пути;
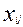 = 1, если i-ый узел связан с j-ым узлом, а в остальных случаях
= 1, если i-ый узел связан с j-ым узлом, а в остальных случаях 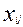 = 0;
= 0;
при ограничениях
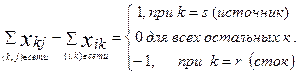
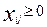 для всех (i,j)
для всех (i,j)  Î сети.
Î сети.
В качестве примера рассмотрим следующую формулировку задачи. Дана сеть 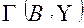 , где
, где 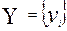 , i- номера узлов,
, i- номера узлов, 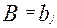 , j-номера ветвей. Дано множество
, j-номера ветвей. Дано множество 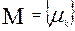 путей, которые могут быть использованы для передачи потоков информации между узлами; даны:
путей, которые могут быть использованы для передачи потоков информации между узлами; даны: 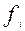 - емкость пути
- емкость пути 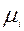 (в числе стандартных каналов) и
(в числе стандартных каналов) и 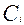 - вес (ценность) пути
- вес (ценность) пути 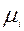 , который определяет целесообразность использования его (по длине, цене и т.п.).
, который определяет целесообразность использования его (по длине, цене и т.п.).
Необходимо определить оптимальную организацию пучков каналов между узлами сети при условии достижения максимума взвешенной суммарной емкости сети:
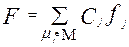 при следующих ограничениях:
при следующих ограничениях:
1) емкости путей не могут принимать отрицательных значений, т.е. 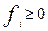 для всех
для всех 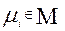 ;
;
2) суммарная емкость путей между произвольной парой (k, l) узлов должна быть равна числу каналов 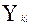 , которые обеспечат требуемое качество обслуживания;
, которые обеспечат требуемое качество обслуживания;
3) для любой ветви 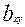 суммарная емкость всех путей, содержащих эту ветвь, не может быть больше емкости ветви, т.е.
суммарная емкость всех путей, содержащих эту ветвь, не может быть больше емкости ветви, т.е. 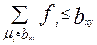 .
.
Одним из наиболее эффективных методов решения задач линейного программирования является симплекс – метод, изучаемый в курсах математики. Однако классическое решение при многочисленных исходных данных требует очень много машинного времени. Поиски методов ускорения процесса решения привели к трем стандартным алгоритмам. Все они основаны на очевидном утверждении, что если кратчайший путь от узла i к узлу проходит через промежуточные узлы 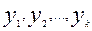 , то кратчайшие пути от узлов
, то кратчайшие пути от узлов 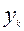 к узлу N являются частями кратчайшего пути
к узлу N являются частями кратчайшего пути 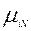 .
.
 2015-01-30
2015-01-30 2150
2150
