Класи задач прийняття багатоцільових рішень за умов невизначеності та ризику

Під ситуацією прийняття багатоцільових рішень будемо ро­зуміти пару {X, F}, де Х= {x₁,..., х_m} — множина рішень органу (су­б'єкта) керування (прийняття рішень):

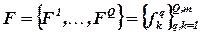
— вектори l функціоналів оцінювання, що визначені на X і приймають рішення з R¹. При заданій ситуації прийняття рішень {X, F} проблема прийняття багатоцільових рішень полягає у тому, що суб'єкт керування повинен обрати одне рішення, оптимальне за обраним критерієм згортки.

Проблема прийняття багатоцільових рішень характеризується трьома чинниками {v, u, w}, де v — метод нормалізації; u— співвідношення пріоритету; w — критерій згортки [50].

Під методом нормалізації "v" будемо розуміти функцію пере­творення F як однозначне відображення в R¹. Нормалізація застосовується для переходу до порівняльних шкал в значеннях функціоналу оцінювання.

Деякі методи нормалізації наведені у табл. 6.1.

Таблиця 6.1. Методи нормалізації

Метод нормализации	Математическая запись
Изменение ингредиента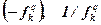
Относительной нормализации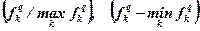
Сравнительной нормализации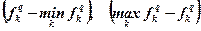
Природной нормализации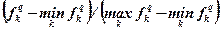
Севиджа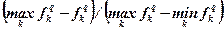

Під відношенням пріоритету "u"будемо розуміти вектор оцінок (u₁,...,u_Q) на компонентах F={F¹,..., F^Q].

Деякі з принципів врахування пріоритету наведені в табл. 6.2.

Таблиця 6.2. Принцип врахування пріоритету

Принцип учёта приоритета	Математическая запись
Линейный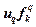
Показательный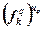
Сокращение размерности задачи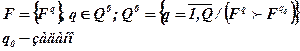

Як правило, критерій згортки являє собою функцію, що відображає R^Q в R¹.

Деякі з критеріїв приведені в табл. 6.3.

Таблиця 6.3. Критерії згортки

Критерии згортки	Математическая запись
Гарантированного результата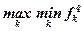
Доминирующего результата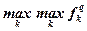
Равности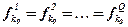
Суммарной эффективности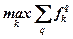
Равномерности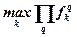

6.3.1. ПЕРША ЗАДАЧА ПРИЙНЯТТЯ БАГАТОЦІЛЬОВИХ РІШЕНЬ ЗА УМОВ РИЗИКУ

Нехай суб'єкт керування має Q (Q > 0) ситуацій прийняття рішень {X,Θ,F¹}, {X,Θ,F²}, {X,Θ,F^Q}, що відрізняються одна від одної функціоналом оцінювання (прибуток, затрати тощо) в заданій інформаційній ситуації I. Необхідно визначити опти­мальне рішення для всіх Q ситуацій прийняття рішень одно­часно. Використання основних чинників {v, u, w} прийняття багато­цільових рішень дозволяє одержати ситуацію прийняття рішень з одним скалярним функціоналом оцінювання для заданої інфор­маційної ситуації I та обраного критерію прийняття рішень.

Пример. Имеем l = 2, X = {x₁, …, x₆}, Θ = {θ₁, θ₂}, F = F⁺, F¹ и F² заданны в виде таких матриц:

; .

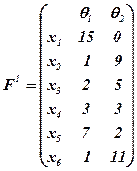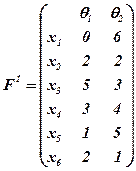Визначена також інформаційна ситуація I = I₅. Суб'єкт ке­рування задає пріоритет з такими ваговими коефіцієнтами: u₁ = 1/4, u₂ = 3/4.

Розв'язання. Візьмемо як основні чинники прийняття рі­шень природну нормалізацію, лінійний метод врахування пріо­ритету та критерій сумарної ефективності. За критерій прий­няття рішень в інформаційній ситуації I₅ обираємо критерій Вальда.

Для природної нормалізації для матриці F¹ маємо:

Враховуючи, що у даному випадку може бути обраний ліній­ний принцип врахування пріоритету (ми допускаємо цю гіпо­тезу), одержимо

т.е.

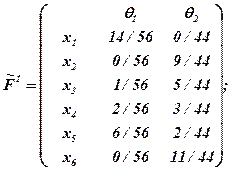
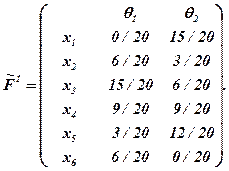
Используя, суммарную згортку 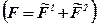получим матрицу функционала оценивания F:

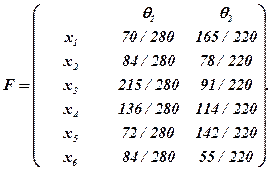
Для критерію Вальда прийняття оптимального рішення про­вадиться так, як це було подано у попередньому розділі.

Одержимо х* = х₄, тобто х₄ є оптимальним максимінним рі­шенням.

6.3.2. ДРУГА ЗАДАЧА ПРИЙНЯТТЯ БАГАТОЦІЛЬОВИХ РІШЕНЬ ЗА УМОВ РИЗИКУ

Припустимо, що суб'єкт керування має Q ситуацій прий­няття рішень (X,Θ, F¹},...,{X,Q,F^Q }, що відрізняються одна від одної функціоналом оцінювання, а також для всіх Q ситуацій прийняття рішень існує одна й та ж сама інформаційна си­туація I та, крім цього, обраний суб'єктом керування критерій прийняття рішень k₀.

Используя критерий принятия решений в каждой из ситуаций, получим ситуацию принятия многоцелевых решений {Х, F}, где F = {F¹, …, F^Q}.

Выбор основных факторов {v, u, w} принятия многоцелевых решений даёт возможность найти многоцелевое оптимальное решение (развязку).

Пример. Условия этого примера такие же, как в предыдущем. В каждой ситуации принятие решений имеет место информационная ситуация I₅; субъектом регулирования, выбранный по критерию принятия решений, - критерий Вальда (принцип гарантированного результата).

Развязка. Выбирая минимум по θ_j, 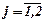для каждого 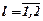и х_k, 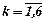вычислим:

;

.

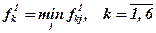Получим ситуацию принятия многоцелевых решений с функционалом F⁺:

Т.е., имеем ситуацию принятия многоцелевых решений {X, F}, F = {F¹, F²}.

В нашем случае, как видно из матрицы, нормализацию использовать нет необходимости (все величины уравнены и находятся в тех же самых диапазонных значений). Что касается соотношения приоритета, то также нет необходимости в его использовании, т.е. u₁ = u₂ =1.

Если по критерию згортки выбрать критерий гарантированного результата, тогда получим единую оптимальную развязку:

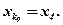
Если по критерию згортки выбрать критерий доминирующего результата или суммарной эффективности, то так же получим в нашем примере ту же самую оптимальную развязку: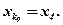

6.3.3. Третья задача принятия многоцелевых решений по условиям риска

Допустим, что субъект регулирования в ситуации принятия решений {X,Θ, F¹} имеет точную информационную ситуацию I, где определена множена критериев принятия решений К_I. Из множены К_I субъект регулирования выделяет (выбирает) не один критерий, а несколько:

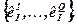
Используя каждый из этих критериев 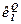к данной ситуации принятия решений, получим для каждой развязки 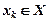вектор оценок:

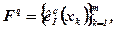
т.е., имеет место ситуация принятия многоцелевых решений, какая оптимальная развязка выбирается аналогично случаю в задаче, которая приведена в 6.3.2.

Пример. Пусть Х = {х₁, х₂, х₃, х₄}, Θ = {θ₁, θ₂, θ₃, θ₄}, а компоненты матрицы значений функціонал оцінювання F⁺ заданий в виде:

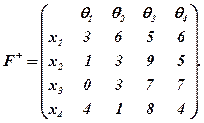
Известны также вероятности положений экономической среды:

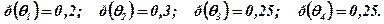
Это отвечает первой информационной ситуации I₁.

Орган регулирования считает целесообразно принять решение по двум критериям: Байеса и модального критерия.

Какое решение их х₁, …, х₄ следует выбрать?

Развязка. Используя критерий Байеса, получим:

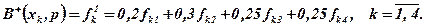
Модальный критерий даёт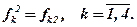

Функционалы оценивания имеют вид:

Застосувавши основні критерії згортки одержимо, що для кожного з цих функціоналів найкращим (оптимальним) рішен­ням буде x_k0 = x₁.

6.3.4. ЧЕТВЕРТА ЗАДАЧА ПРИЙНЯТТЯ БАГАТОЦІЛЬОВИХ РІШЕНЬ ЗА УМОВ РИЗИКУ

Припустимо, що суб'єкт керування має ситуацію прийняття рішень { X, Θ, F }та нехай виділено Q інформаційних ситуацій. Для кожної інформаційної ситуації органом управління виді­ляється один певний критерій прийняття рішень

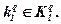
Застосувавши кожен з обраних критеріїв у ситуації, { X, Θ, F } одержимо ситуацію прийняття багатоцільових рішень.

Приклад. Нехай Х = {х₁, х₂, х₃, х₄, х₅, x₆}, Θ = {θ₁, θ₂} функціонал оцінювання F¹ заданий першою матрицею, що наведена у при­кладі 6.3.1. Економічне середовище характеризується першою інформаційною ситуацією з імовірностями станів р (θ₁) = 3/4, p (θ₂) = 1/4 та четвертою інформаційною ситуацією. Суб'єктом керування також обрані наступні критерії прийняття рішень: критерій Байєса в I₁ і критерій Бернуллі-Лапласа в I₄.

Розв'язання. Застосувавши обрані критерії, одержимо си­туацію прийняття багатоцільових рішень, де

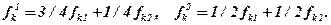
Запишемо функціонали оцінювання

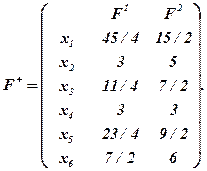
В одержаній ситуації прийняття багатоцільових рішень при u₁ = u₂ = 1 і відсутності нормалізації єдиним оптимальним роз­в'язком для всіх критеріїв згортки, окрім критерію рівності, є x₁.