Пусть событие 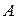 – среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятность
– среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятность 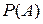 равна отношению
равна отношению 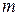 – числа исходов, благоприятствующих событию
– числа исходов, благоприятствующих событию 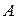 , к
, к 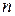 – числу всех элементарных исходов:
– числу всех элементарных исходов:
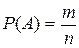 .
.
Общее число всех всевозможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 книг из 10 имеющихся, т.е. числу сочетаний из 10 элементов по 6 (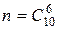 ).
).
Определим 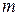 – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию 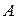 . Четыре книги можно взять из 7 книг по математике
. Четыре книги можно взять из 7 книг по математике 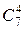 способами; при этом остальные (
способами; при этом остальные (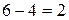 ) книги должны быть не по математике. Взять же 2 книги нематематические из (
) книги должны быть не по математике. Взять же 2 книги нематематические из (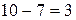 ) нематематических книг можно
) нематематических книг можно 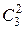 способами. Следовательно, число благоприятствующих исходов
способами. Следовательно, число благоприятствующих исходов 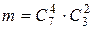 . Таким образом, учитывая, что
. Таким образом, учитывая, что 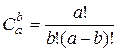 , получаем:
, получаем:
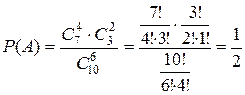 .
.
Ответ: 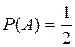 .
.
 2015-01-30
2015-01-30 308
308








