Решение. Пусть гипотеза - «случайная величина Х распределена по нормальному закону»

Пусть гипотеза 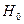- «случайная величина Х распределена по нормальному закону». Для проверки этой гипотезы распределим значения с.в. Х по интервалам, объединив первый интервал со вторым, т.к. оба интервала являются малочисленными. Далее расширим крайние интервалы значений с.в. Х до 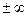, и высчитаем теоретические частоты попадания значений с.в. в каждый промежуток по формуле:

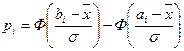, где 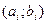- границы интервала.

Статистический ряд распределения тогда примет вид:

Интервал		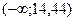(14,44; 16,16)	(16,16; 17,88)	(17,88; )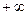
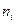
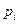
	0,1357	0,3882	0,315	0,1611

Итак,

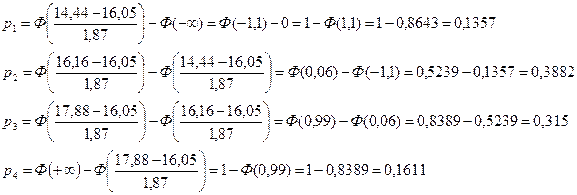
Умножим полученные теоретические вероятности на n=30, получим теоретические частоты попадания с.в. Х в каждый из промежутков:

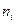
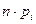
	4,07	11,65	9,45	4,83

Вычислим наблюдаемое значение критерия Пирсона по формуле:

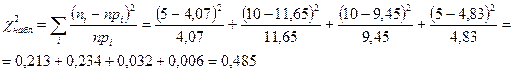
По таблице распределения Пирсона найдем критическое значение критерия, учитывая число степеней свободы: k-2-1=4-2-1=1. Тогда по таблице:

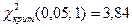
Таким образом, сравнивая значения 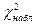и 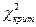, делаем вывод, что гипотезу о нормальном распределении необходимо принять на уровне значимости 0,05.

Задача 13.3.1. Определите коэффициенты выборочного уравнения регрессии .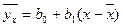

Решение. Коэффициенты регрессии рассчитываются по формулам:

,

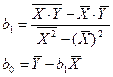только в качестве X в данном случае будет выступать разность .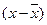

Составим вспомогательную таблицу для расчета всех необходимых значений:

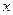
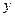
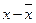
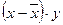
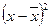
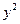
			-19,07	-209,73	363,54	121,00
	12,1	-26,07	-315,41	679,47	146,41
	12,8	-22,07	-282,45	486,94	163,84
	13,8	-13,07	-180,32	170,74	190,44
	14,2	-10,07	-142,95	101,34	201,64
	14,6	-15,07	-219,97	227,00	213,16
	14,8	-5,07	-74,99	25,67	219,04
	15,5	-6,07	-94,03	36,80	240,25
	15,7	-6,07	-95,25	36,80	246,49
	15,8	3,93	62,15	15,47	249,64
	15,9	-0,07	-1,06	0,00	252,81
		-41,07	-657,07	1686,47	256,00
		-32,07	-513,07	1028,27	256,00
		6,93	110,93	48,07	256,00
	16,1	1,93	31,13	3,74	259,21
	16,2	0,93	15,12	0,87	262,44
	16,3	7,93	129,31	62,94	265,69
	16,4	3,93	64,51	15,47	268,96
	16,4	3,93	64,51	15,47	268,96
	16,5	-8,07	-133,10	65,07	272,25
	16,5	4,93	81,40	24,34	272,25
	16,7	13,93	232,69	194,14	278,89
	16,7	17,93	299,49	321,60	278,89
	17,2	3,93	67,65	15,47	295,84
	17,6	13,93	245,23	194,14	309,76
		10,93	196,80	119,54	324,00
	18,2	24,93	453,79	621,67	331,24
	18,5	20,93	387,27	438,20	342,25
	19,1	28,93	552,63	837,14	364,81
	19,6	33,93	665,09	1151,47	384,16
сумма	2012,00	480,20	0,00	740,29	8987,87	7792,32
среднее	67,07	16,01	0,00	24,68	299,60	259,74

Теперь можно вычислить коэффициенты регрессии:

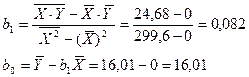
Итак, уравнение регрессии Y на 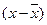имеет вид:

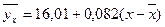
Задача 13.3.2. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.

Решение. Существует несколько методов определения наличия корреляционной связи между двумя изучаемыми признаками. Мы используем метод факторных группировок и регрессионно-корреляционный методы.

Как уже мы делали в задании 13.1.1, разместим все значения изучаемого признака по 5 интервалам. Только сейчас объясняемая переменная – сумма прибыли, а объясняющая – выпуск продукции.

Выпуск продукции, интервал значений	Количество предприятий в группе	Суммарная прибыль по группе	Средняя прибыль на одно предприятие группы
[26; 41]
[41; 56]			49,75
[56; 71]			65,67
[71; 86]
[86; 101]			94,25

По построенной таблице видно, что чем выше значение выпуска продукции, тем выше и значение средней прибыли по одному предприятию, то есть имеет место прямая положительная связь между изучаемыми признаками.

Проверим сделанный вывод, построив диаграмму рассеяния:

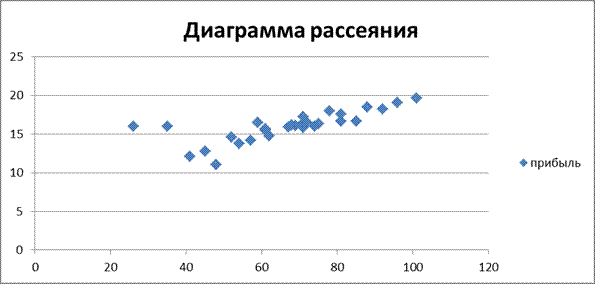
Анализируя характер расположения точек на диаграмме, можно предположить, что связь между изучаемыми факторами – линейная, прямая, причем в среднем все точки приближаются к прямой, уравнение которой мы уже нашли: 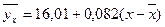- это уравнение линейной регрессии.

Задача 13.3.3. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.