а) По условию случайная величина 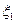 имеет равномерное распределение. Математическое ожидание и дисперсия такой с.в. можно найти по формулам:
имеет равномерное распределение. Математическое ожидание и дисперсия такой с.в. можно найти по формулам:
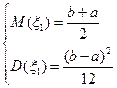
Из этих соотношений найдем границы отрезка [a; b]:
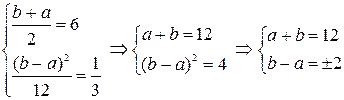
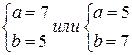
Таким образом, случайная величина 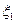 распределена равномерно на отрезке [5; 7]. Запишем ее функцию распределения:
распределена равномерно на отрезке [5; 7]. Запишем ее функцию распределения:
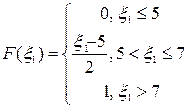
Тогда вероятность попадания с.в. в заданный отрезок равна:
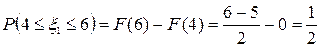
б) Закон распределения пуассоновской с.в. имеет вид:
| … | m | … | ||||
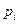
| 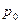
| 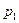
| 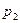
| 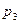
| … | 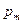
| … |
Вероятности 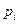 вычисляются по формуле:
вычисляются по формуле: 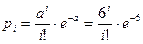 .
.
Тогда искомая вероятность равна:
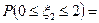
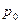 +
+ 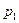 +
+ 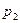 .
.
Итак,
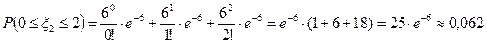
в) с.в. 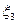 имеет показательное распределение, значит, ее функция распределения имеет вид:
имеет показательное распределение, значит, ее функция распределения имеет вид:
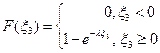
Здесь 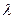 - параметр распределения, определяемый из соотношения:
- параметр распределения, определяемый из соотношения:
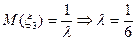
Тогда искомая вероятность вычисляется по формуле:
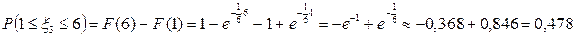
 2015-01-30
2015-01-30 861
861








