Стержнем и шкивами

Точку О, являющуюся серединой расстояния между осями шкивов, примем

за начало системы координат. Используя теоре­му о движении центра масс, составим

дифференциальное уравне­ние движения стержня в проекциях на ось ОХ в указанной систе­ме

координат:

mX_c=fN₁-fN_2t (2.1)

где Х_с- координата центра тяжести стержня.

Находим силы реакции связей N₁ и N₂ следующих уравнений равновесия стержня:

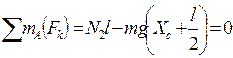
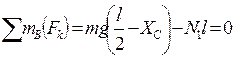
где l - расстояние между центрами шкивов. То есть

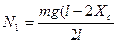
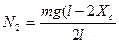
Подставив значения N₁ и N₂ в уравнение (2.1), после преобра­зований получим:

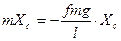(2.2)

Сократив обе части равенства на т и вводя обозначениеK² = 2fg./l, приведем уравнение (2.2) к виду:

Х_с+К²Х_с=0 (2.3)

Как известно, общее решение этого дифференциального урав­нения имеет вид:

Х_с = С₁ sin kt + cos kt,

где С₁ и С₂ - постоянные интегрирования.

Если вместо постоянных C₁ и С₂ ввести постоянные А и α та­кие, что

С] = A cos а, С2 = A sin а, то получим:

Х_c =. A (sin kt • cos a + cos kt• sin a)

Или

X_c = A sin(kt + a) (2.4)

Дифференцируя это выражение по времени, получим:

Х_с = Ak cos(kt + a) (2.5)

Так как стержень начинает свое движение из состояния покоя при начальном смещении центра тяжести С от начала координат на величину Х₀, то начальными условиями для уравнений (2.4) и (2.5) являются:

t = 0,X_c = X_o,X_c = 0.

С учетом этих начальных условий из уравнений (2.4) и (2.5) получим:

Asinα = X₀,

Akcosα= 0. Откуда α=π/2, А= Х₀.

Тогда уравнение (2.4) примет конечный вид:

X_c = X₀coskt. (2.6)

Уравнение (2.6) представляет, собой уравнение гармоническо­го колебания стержня. Период колебаний его определяется по формуле:

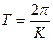
(2.7)

Или с учетом 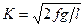получим:

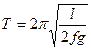
Таким образом, зная период колебании стержня, расстояние между шкивами, можно определить коэффициент трения сколь­жения между материалами стержня и шкивов.