Используемые в теории надежности

Подавляющее большинство производственных процессов в строительстве, как известно, в силу их специфики носят характер случайных процессов. Достаточно упомянуть, например, все технические нормы, основанные на ЕНиР, технологические процессы и операции, лежащие в основе выполнения строительно-монтажных работ. Поэтому для количественного анализа случайных процессов необходимо знание закона их распределения (функции или плотности распределения), математического ожидания и дисперсии случайных величин [7].

1.Закон равномерной плотности.

Он справедлив для тех случаев, когда случайное событие лежит в определенном временном интервале, причем появление его в любой момент времени равновероятно.

Например, при производстве монтажных работ методом «монтажа с колёс» доставка на объект сборных железобетонных конструкций должна осуществляться по специальным графикам с жестко установленным интервалом T минут. Необходимо установить закон распределения времени ожидания монтажного звена t_ож=х, если монтажники освободятся в произвольный момент времени. В данном случае ясно, что благоприятное событие (т.е. прибытие трейлера с конструкциями) распределено равномерно на временном интервале T и плотность распределения постоянна, т.е. 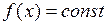, на всем участке действия закона от 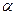до 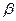, как это видно из следующего рисунка (рис.13 а), б)).

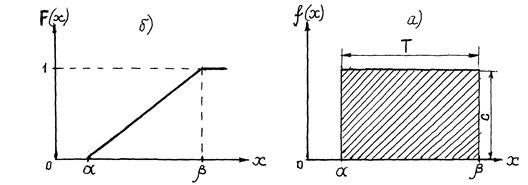
Рис. 13. Графическое выражение закона равномерной плотности.

Поскольку событие заведомо произойдет на интервале времени T, то вероятность его равна 1. Отсюда плотность распределения

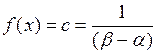, а интегральная функция распределения [т.е. F(x)=P( 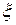<x) – вероятность того, что случайная величина 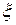будет меньше числа х]

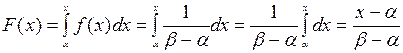
Для количественного анализа случайных процессов, кроме рассмотренных функций распределения необходимо также знание и таких характеристик, как математическое ожидание M и дисперсия D.

Так, для закона равномерного распределения математическое ожидание

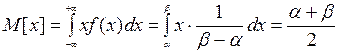
Соответственно, дисперсия в этом случае определяется по формуле

=

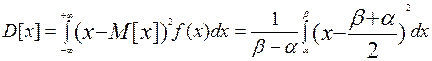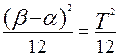
Зная дисперсию, легко определить среднее квадратичное отклонение:

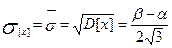
Указанные формулы M[x] и D[x] справедливы для непрерывных случайных величин.

Для дискретных случайных величин в теории вероятностей даются следующие формулы:

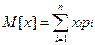
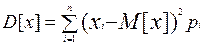
2. Закон экспоненциального или показательного распределения.

Распределение по этому закону является одним из наиболее распространенных в строительном производстве, не только благодаря своей простоте, но и соответствия характера распределения отказов в реальных производственных системах, состоящих из большого количества элементов.

Функция распределения (интегральная) экспоненциального закона имеет следующий вид:

,

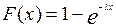где

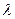– интенсивность отказов

А плотность распределения соответственно равна

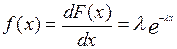
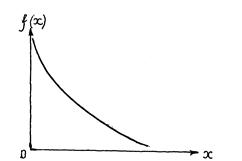
Графически эта зависимость выражается известной кривой (рис.14):

Математическое ожидание для показательной функции имеет вид:

,

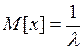а дисперсия:

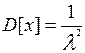
Нетрудно заметить, что D[x]=(M[x])²

Это свойство экспоненциального закона распределения можно использовать для приблизительной оценки при описании экспериментальных данных (с точки зрения соответствия их экспоненциальному закону).

3. Закон нормального (Гауссова) распределения.

В строительстве этому закону соответствуют распределения таких фактических данных, как, например, нормы выработки рабочих и машин, продолжительность технологических этапов, сроки строительства типовых объектов и ряд др.

Плотность распределения нормального закона записывается в следующем виде:

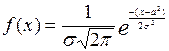
где

a=M[x] – математическое ожидание;

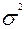=D[x] – дисперсия распределения.

Кривая плотности распределения имеет вид (рис.15):

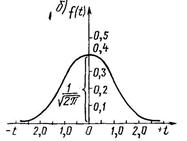
Рис. 15. График нормального закона распределения.

Вероятность попадания случайной величины, распределенной по нормальному закону, на заданный интервал измерения параметра x от 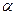до 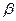обычно определяется интегрированием плотности распределения, т.е.

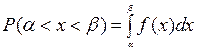
При этом в процессе решения используется известная функция или так называемый оператор Лапласа:

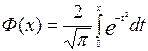
4. Закон распределения Пуассона. - наиболее успешно используется для определения вероятности дискретных событий или появления потока событий. Если независимые события следуют с известной средней частотой 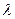t=a, то вероятность того, что за какой-то отрезок времени t событие наступит n раз, определяется законом Пуассона:

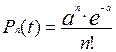
Как видно из формулы, особенностью пуассоновского распределения является его зависимость лишь от одного параметра 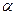– математического ожидания числа наступления события за время t. В теории вероятностей доказывается, что дисперсия случайной величины, распределенной по закону Пуассона, так же равна 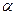, т.е. D[t]= 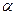. Это обстоятельство упрощает количественный анализ пуассоновских процессов. Интересно также и то, что, как видно из графика (рис.16), при больших 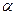пуассоновское распределение по своему характеру близко к нормальному.

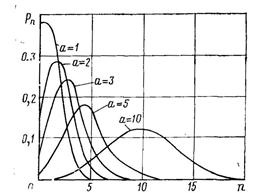
Рис.16. Пример распределения Пуассона.

В строительстве законом Пуассона описываются такие, например, события, как число отказов, возникающих при монтаже здания или сооружения в течение суток, месяца, года или количество случаев поломок землеройных и землеройно-транспортных машин при производстве земляных работ, взятых за соответствующий период времени (месяц, квартал, год и т.д.).

Кроме рассмотренных, существует еще множество других распределений – бета, гамма, Стьюдента, Фишера, Релея и др., которые значительно реже используются при анализе строительных процессов и поэтому нами не рассматриваются.