Иллюстрация, приведенная в начале этой статьи, помещена в любопытной книге Сэма Лойда «Энциклопедия головоломок» (Нью‑Йорк, 1914). Это большой том, заключающий 5000 разнообразных задач и развлечений, из которых тысяча иллюстрирована. Рисунок интересующей нас игры сопровождается следующим текстом.
«Давнишние обитатели царства смекалки помнят, как в начале 70‑х годов я заставил весь мир ломать голову над коробкой с подвижными шашками, получившей известность под именем „игры в 14–15“. Пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14‑я и 15‑я были переставлены, как показано на прилагаемой иллюстрации. Задача состояла в том, чтобы, последовательно передвигая шашки, привести их в исходное положение, причем, однако, порядок шашек 14‑й и 15‑й должен быть исправлен.
Премия в 1000 долларов, предложенная за первое правильное решение этой задачи, никем не была заслужена, хотя тысячи людей уверяли, что выполнили требуемое. Все принялись без устали решать эту задачу. Рассказывали забавные истории о торговцах, забывавших из‑за этого открывать свои магазины, о почтенных чиновниках, целые ночи напролет простаивавших под уличным фонарем, отыскивая путь к решению. Непостижимой особенностью игры было то, что никто не желал отказываться от поисков решения, так как все чувствовали уверенность в ожидающем их успехе. Штурманы, говорят, из‑за игры сажали на мель свои суда, машинисты проводили поезда мимо станций, торговля была деморализована. Фермеры забрасывали свои плуги, – один из таких моментов изображен на прилагаемой иллюстрации.
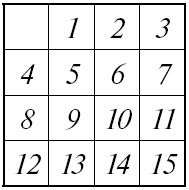
К задаче 2‑й
Вот несколько новых задач, кроме той, которая приведена выше.
Задача 2‑я. Исходя из расположения, показанного на схеме I, привести шашки в правильный порядок, но со свободным полем в левом верхнем углу (см. чертеж). Задача 3‑я. Исходя из расположения схемы I, поверните коробку на четверть оборота и передвигайте шашки до тех пор, пока они не примут расположения чертежа.
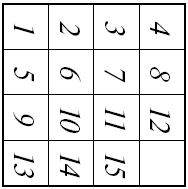
К задаче 3‑й
Задача 4‑я. Передвижением шашек превратите коробку в „магический квадрат“, а именно: разместите шашки так, чтобы сумма чисел была во всех направлениях равна 30».
РЕШЕНИЯ
Расположение задачи 2‑й может быть получено из начального положения следующими 44 ходами:
14, 11, 12, 8, 7, 6, 10, 12, 8, 7
4, 3, 6, 4, 7, 14, 11, 15, 13, 9
12, 8, 4, 10, 8, 4, 14, И, 15, 13
9, 12, 4, 8, 5, 4, 8, 9, 13, 14
10, 6, 2, 1.
Расположение задачи 3‑й достигается следующими 39 ходами:
14, 15, 10, 6, 7, 11, 15, 10, 13, 9
5, 1, 2, 3, 4, 8, 12, 15, 10, 13
9, 5, 1, 2, 3, 4, 8, 12, 15, 14
13, 9, 5, 1, 2, 3, 4, 8, 12.
Магический квадрат с суммою 30 получается после ряда ходов:
12, 8, 4, 3, 2, 6, 10, 9, 13, 15
14, 12, 8, 4, 7, 10, 9, 14, 12, 8
4, 7, 10, 9, 6, 2, 3, 10, 9, 6
5, 1, 2, 3, 6, 5, 3, 2, 1, 13
14, 3, 2, 1, 13, 14, 3, 12, 15, 3.
Приведем замечание немецкого математика Шуберта о числе возможных задач при «игре в 15».
«Сколько всего возможно задач, т. е. сколько различных расположений можно дать 15 шашкам, причем каждый раз пустое поле расположено справа внизу? Чтобы определить, сколько перестановок можно получить с помощью 15 предметов, начнем с 2‑х предметов: а и Ь. Они могут дать лишь две перестановки, именно – ab и Ьа. При трех предметах имеется уже втрое больше перестановок, т. е. 6, так как предмет „а“ может быть поставлен перед Ьс и перед cb, и, кроме того, имеются еще две перестановки, начинающиеся с Ь, и две, начинающиеся с с. Отсюда можно заключить, что четыре предмета а, Ь, с, d могут дать вчетверо большее число различных перестановок, т. е. 4 × 3 × 2 = 24 перестановки. Продолжая так, можно найти, что 15 шашек допускают всего
2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 × 11 × 12 × 13 × 14 × 15
перестановок. Вычислив это произведение, мы найдем для числа задач игры внушительное число:
1 биллион 307 674 миллиона 365 000».
Из этого огромного числа задач ровно половина принадлежит к разрешимым и столько же – к неразрешимым. Заметим еще, что если бы возможно было ежесекундно давать шашкам новое положение, то, чтобы перепробовать все возможные расположения, потребовалось бы, при непрерывной работе круглые сутки, свыше 40 000 лет.
 2015-01-07
2015-01-07 501
501








