2015-01-07
815
1.Описать системой команд, функциональной таблицей и диаграммой переходов работу машины Тьюринга, реализующую заданный вариантом алгоритм. Начальная и конечная конфигурации стандартны.
2. Проверить модель алгоритма на множестве тестовых примеров. Привести последовательности конфигураций машины Тьюринга, заданной в предыдущем пункте, для различных тестовых исходных слов.
Варианты заданий
1. Реализовать функцию арифметическое вычитание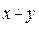 
в унарном коде.
2. Реализовать функцию выбор максимального из двух чисел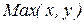 
над числами в унарном коде.
3. Реализовать функцию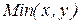 
над числами в унарном коде.
4. Реализовать функцию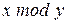 
над числами в унарном коде.
5. Реализовать функцию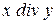 
над числами в унарном коде.
6. Реализовать функцию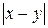 
над числами в унарном коде.
7. Реализовать функцию выбор аргумента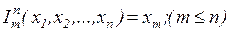 
над числами в унарном коде.
8. Реализовать вычисление предиката X>Y в унарном коде с сохранением (восстановлением) исходных данных.
9. Реализовать вычисление предиката X=Y в унарном коде с сохранением (восстановлением) исходных данных.
10. Реализовать вычисление предиката “x - четное число” в двоичном коде.
11. Реализовать алгоритм в алфавите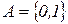 
, меняющий местами первую и последнюю буквы слова.
12. Реализовать алгоритм над алфавитом 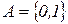, меняющий местами первый ноль и последнюю единицу.
13. Реализовать операцию копирование в алфавите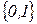 
, то есть получить из слова 
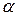слово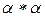 
.
14. Реализовать алгоритм над алфавитом 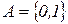, который выдает единицу, если в исходном слове только парные нули и ноль в противном случае.
15. Реализовать алгоритм в алфавите 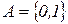, который переставляет буквы в слове 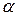так, чтобы сначала шли все нули, потом – единицы.
16. Реализовать алгоритм, конструирующий в алфавите 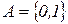слова вида 
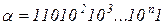, где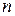 
- произвольное натуральное число.
17. Реализовать алгоритм, реализующий функцию циклический сдвиг двоичного числа на одну ячейку.
18. Реализовать алгоритм в алфавите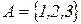 
, анализирующий последовательность цифр в слове и выдающий «+», если цифры образуют неубывающую последовательность, и «–» в противном случае.
19. Реализовать выделение подстроки, заключенной между двумя символами 
(первая пара) в алфавите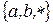 
. Если последовательность 
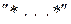отсутствует на ленте, стереть все.
20. В слове 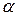в алфавите 
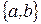стереть все, кроме 
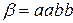. Если такой последовательности нет, все стереть.
21. Реализовать алгоритм над алфавитом 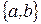, переставляющий буквы в обратном порядке.
22. Реализовать предиката «в слове a в алфавите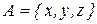 
есть пара букв ‘ yy ’».
23. Реализовать алгоритм в алфавите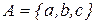 
, производящий в слове a алфавита замену всех вхождений буквы а на букву б.
24. Реализовать алгоритм в алфавите 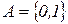для вычисления логической функции 
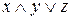, где x,y,z принимают значение 0 или 1.
25. Реализовать алгоритм в алфавите 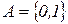для вычисления логической функции 
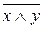, где x,y,z принимают значение 0 или 1.
Контрольные вопросы
11. Дать определение машины Тьюринга и ее составляющим.
12. Перечислить и определить способы описания МТ.
13. Какие операции выполняются в каждом такте работы МТ?
14. Дать определение конфигурации МТ.
15. Какие начальные и конечные конфигурации называют стандартными и как они обозначаются?
16. Что такое функция, правильно вычислимая по Тьюрингу?
17. Какие способы композиции МТ существуют, как они применяются и обозначаются?
18. Формулировка тезиса Тьюринга; можно ли его доказать строго?
Лабораторная работа № 3
