Если 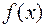 – бесконечно малая функция в точке
– бесконечно малая функция в точке 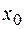 , то
, то 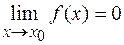 .
.
Если 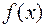 – бесконечно большая функция в точке
– бесконечно большая функция в точке 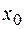 , то
, то 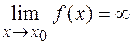 .
.
В таблице 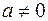 – произвольное число.
– произвольное число.
| Неопределенности: | |||||
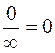
| 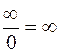
| 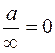
| 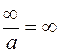
| 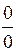
| 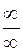
|
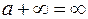
| 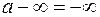
| 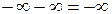
| 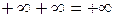
| 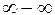
| |
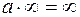
| 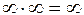
| 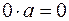
| 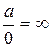
| 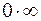
| |
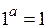
| 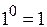
| 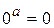
| 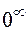
| 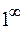
| |
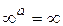 ,
если ,
если 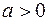
| 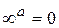 ,
если ,
если 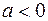
| 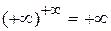
| 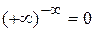
| 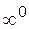
| 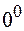
|
2.5. Отыскание асимптот графика функции 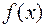
(1) Прямая 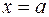 является вертикальной асимптотой функции
является вертикальной асимптотой функции 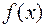 , если хотя бы один из односторонних пределов
, если хотя бы один из односторонних пределов 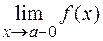 и
и 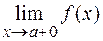 равен
равен  или
или 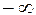 . Значения
. Значения 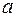 ищем среди точек разрыва области определения и ее конечных границ.
ищем среди точек разрыва области определения и ее конечных границ.
(2) При 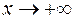 (при
(при 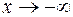 ) у функции
) у функции 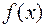 имеется горизонтальная асимптота, если существует конечный предел
имеется горизонтальная асимптота, если существует конечный предел 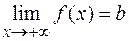
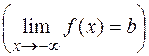 . Тогда
. Тогда 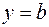 – искомая горизонтальная асимптота при
– искомая горизонтальная асимптота при 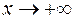 (при
(при 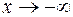 ).
).
(3) Если при 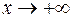 (при
(при 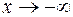 ) нет горизонтальных асимптот, то возможно найти наклонные асимптоты функции
) нет горизонтальных асимптот, то возможно найти наклонные асимптоты функции 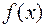 . Для этого необходимо вычислить пределы
. Для этого необходимо вычислить пределы 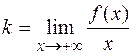 и
и 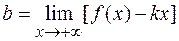 . Если они существуют, причем
. Если они существуют, причем 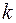 и
и 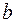 конечны, то прямая
конечны, то прямая 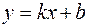 является наклонной асимптотой при
является наклонной асимптотой при 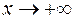 . Аналогично находится наклонная асимптота и при
. Аналогично находится наклонная асимптота и при 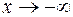 .
.
 2015-01-07
2015-01-07 681
681








