Пусть 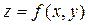 - функция двух переменных.
- функция двух переменных.
Две частные производные первого порядка:
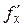 и
и 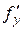 (или
(или 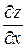 и
и 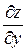 ).
).
Четыре частных производных второго порядка:
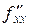 ,
, 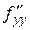 ,
, 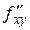 и
и 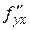 (или
(или 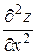 ,
, 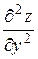 ,
, 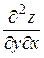 и
и 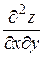 ).
).
Если смешанные производные 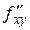 и
и 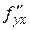 непрерывны в некоторых точках, то в этих точках выполняется равенство:
непрерывны в некоторых точках, то в этих точках выполняется равенство: 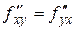 .
.
Аналогично определяются производные высших порядков.
Дифференциал первого порядка:
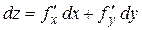 .
.
Дифференциал второго порядка:
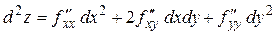 .
.
 2015-01-07
2015-01-07 592
592








