2015-01-07
434
Алгоритм нахождения условных экстремумов функции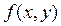 
при условии, заданном в виде 
.
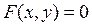1. Составляем функцию Лагранжа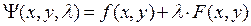 
.
2. Находим первые производные функции Лагранжа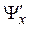 
и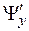 
.
3. Решая систему уравнений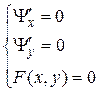 
, находим подозрительные на условный экстремум точки 
и соответствующие l.
4. Находим вторые частные производные функции Лагранжа: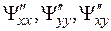 
и составляем выражение 
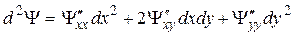, в котором dx, dy – произвольные переменные приращения.
5. Полученные в п.3 точки и l подставляем в выражение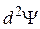 
.
6. Находим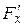 
и 
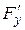. Составляем равенство 
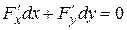. Подставляем каждую из подозрительных точек (из п.3) и выражаем 
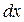через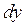 
или 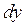через .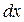
7. Подставляем найденное выражение из п.6 в выражение 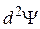из п.5 и приводим к виду 
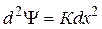или 
8. Если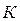 
>0, то в данной точке условный минимум; если 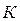<0, то в данной точке условный максимум. Вычисляем значение функции 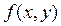в каждой точке условного экстремума.
