Повторение испытаний

Пусть производится 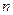испытаний, причём вероятность некоторого события 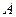в каждом испытании не зависит от исходов других испытаний, постоянна и равна .

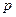Тогда вероятность того, что событие 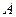наступит ровно 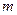раз в 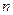независимых испытаниях, определяется по формуле Бернулли

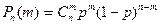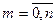, . (10)

Пример 14. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырёх или три партии из шести (ничьи во внимание не принимаются)?

Решение. Поскольку игроки равносильные, то вероятность выигрыша партии всегда постоянна и равна 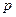=0,5. Здесь применима формула Бернулли (10).

Найдем вероятность того, что две партии из четырёх будут выиграны:

.

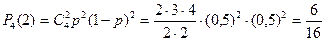Далее найдем вероятность того, что будут выиграны три партии из шести:

.

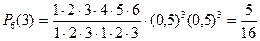Поскольку 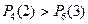, то вероятнее выиграть две партии из четырёх, чем три из шести.