Случайные величины

Функцией распределения 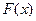случайной величины 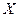называют вероятность того, что случайная величина 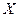примет значение, строго меньшее, чем :

.

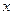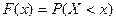Её основные свойства:

1. .

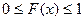2. .

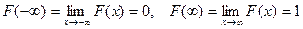3. .

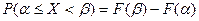Плотностью распределения непрерывной случайной величины 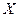называется производная её функции распределения

.

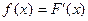Её основные свойства:

1. .

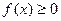2. .

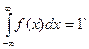3. .

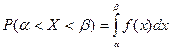Математическим ожиданием 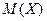непрерывной случайной величины 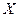называется интеграл

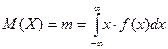. (11)

Дисперсией 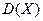непрерывной случайной величины 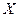называется математическое ожидание квадрата её отклонения от своего математического ожидания

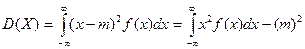. (12)

Средним квадратическим отклонением (СКО) случайной величины 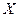называется корень квадратный из её дисперсии

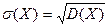. (13)

Квантилем порядка 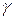называется такое значение 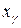случайной величины 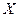, при котором её функция распределения принимает значение, равное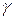

.

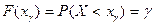Пример 15. Функция распределения спроса на некоторый продуктовый товар для различных микрорайонов города задается выражением:

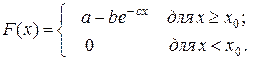
Требуется найти:

1. Плотность распределения вероятности.

2. Параметры 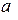и .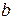

3. Математическое ожидание, дисперсию, среднее квадратическое отклонение спроса.

4. Вероятность того, что в наудачу выбранном микрорайоне спрос находится в пределах от значения 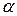до .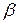

5. Размер спроса, который для случайного выбранного микрорайона может быть превзойден с вероятностью .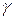

Параметры 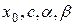(в млн. руб), 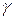приводятся в таблице 5.

Таблица 5

Значения параметров
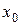
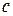
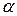
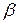
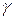
				0,6

Решение.

1. Плотность распределения вероятностей является производной функции распределения вероятностей, поэтому:

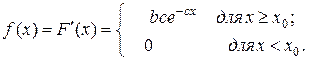
2. Найдем параметр 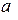. Функция распределения обладает следующим свойством: 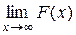=1.

Вычислим предел = .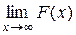

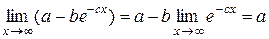Отсюда 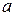=1.

Далее определим параметр 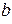. Интеграл от плотности вероятности по области реализации случайной величины равен единице (свойство 2). В соответствии с условиями задачи спрос как случайная величина изменяется в пределах от 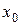до 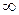. Поэтому, находя несобственный интеграл, имеем

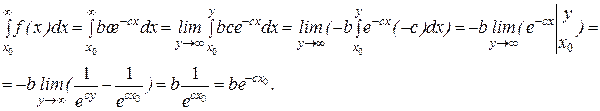
Таким образом, = .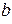

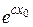3. Вычислим математическое ожидание спроса по формуле (11) с учетом того, что = :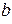

.

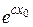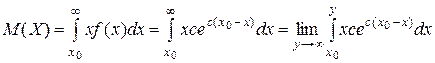Найдем интеграл методом интегрирования по частям. Пусть .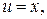

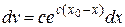Тогда .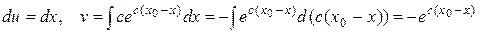

Применяя формулу интегрирования по частям, получим

.

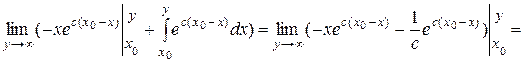
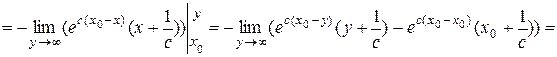
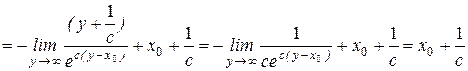Подставив в полученное выражение численные значения параметров, найдём:

.

По формуле (12) определим дисперсию спроса. Вначале вычислим несобственный интеграл

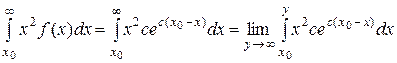
также методом интегрирования по частям. Пусть .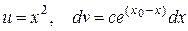

Тогда

,

.

Последний интеграл уже найден при вычислении 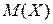, поэтому можно записать:

.

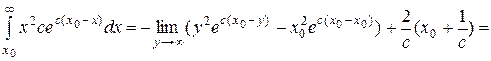
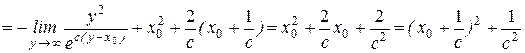Отсюда окончательно получаем: 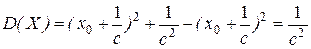. После подстановки численных значений параметров, находим

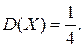
Среднеквадратическое отклонение вычисляется по формуле (13):

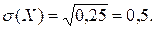
4. Вероятность нахождения случайной величины в заданном интервале можно найти, используя функцию распределения (свойство 3)

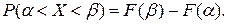
При 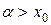получаем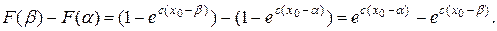

Подставляя численные значения параметров, имеем: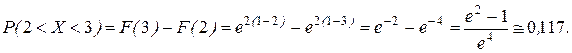

5. Величина 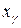, определяемая равенством 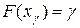, называется квантилем порядка .

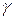В задаче требуется найт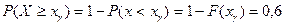и или .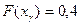

Таким образом, требуется найти квантиль порядка 0,4. Зная функцию распределения спроса, запишем требуемое равенство: или 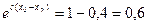. Логарифмируя это равенство 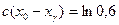, найдем 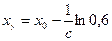. Отсюда, 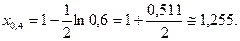Таким образом, спрос в случайно выбранном микрорайоне с вероятностью 0,6 будет больше 1,255 (млн. руб).