2015-01-07
2273
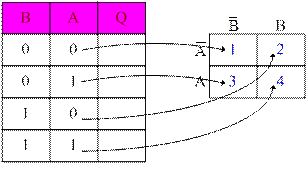
Четыре квадрата соответствуют четырем возможным комбинациям А и В в таблице истинности с двумя переменными. При этом квадрат 1 соответствует произведению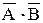 
, квадрат 2 соответствует произведению 
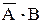, квадрат 3 - 
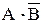, квадрат 4 - 
.
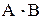Например.
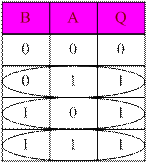
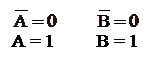
Из этой таблицы истинности видно, что по известным правилам получаем логическое выражение в ДНФ.
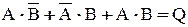
В записи карт Карно соседние единицы объединяются в контуры группами по 2, 4, 8, и т. д. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Каждый контур представляет собой новый член упрощенного логического выражения. Возьмем сначала нижний контур, заметим, что переменная А здесь встречалась в комбинации с В и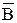 
. В соответствии с правилами алгебры логики В и 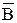дополняют друг друга и тогда в нижнем контуре остается только первый член А. В другом контуре вместе с В встречается так же А и 
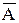, что также является дополнением и поэтому во втором контуре остается один член В. Полученное таким образом в каждом контуре выражение объединяются логической функцией «сложение». В результате получим упрощенное выражение А + В.
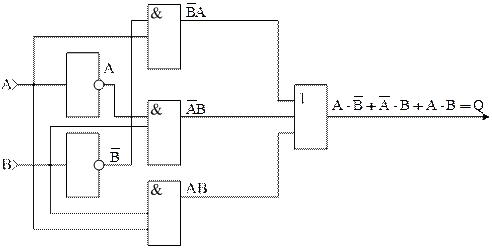
Последовательность операций, при упрощении логических выражений с помощью карт Карно:
· Получение логического выражения в ДНФ, как правило, из таблицы истинности.
· По этому логическому выражению заносятся единицы в соответствующие клетки карты Карно.
· Эти единицы в карте Карно объединить в контуры, охватывающие 2, 4, 6 и т. д. соседних единиц.
· Проводим упрощение путем исключения членов в контуре дополняющих друг друга.
· Полученное таким образом в каждом контуре выражения объединяются логической функцией «ИЛИ».
