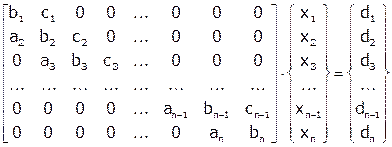
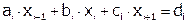 , где
, где 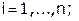
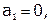
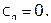
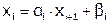 , где
, где 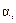 и
и 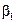 - прогоночные коэффициенты.
- прогоночные коэффициенты.
Первое уравнение.
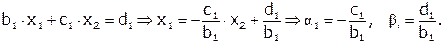
Второе уравнение.
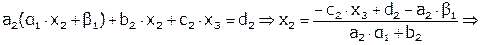
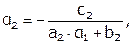
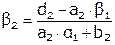 .
.
Обозначим 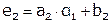 , тогда
, тогда 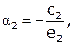
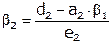 .
.
Третье уравнение.
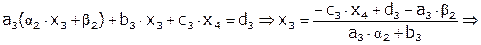
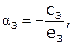
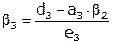 , где
, где 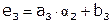 .
.
i-тое уравнение.
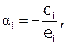
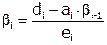 , где
, где 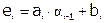 .
.
Вычисление 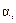 и
и 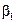 для
для 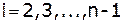 – прямая прогонка.
– прямая прогонка.
Из уравнений n и n-1 имеем:
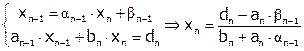 .
.
Обратная прогонка состоит в последовательном вычислении неизвестных с помощью прогоночных коэффициентов:
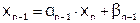 ,
,
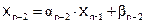 ,
,
…,
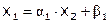 .
.
Алгоритм решения СЛАУ методом прогонки:
1) 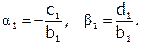
2) Для 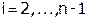 :
:
3) 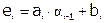 .
.
4) 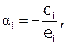
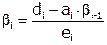 .
.
5) 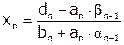 .
.
6) Для 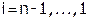 (шаг -1):
(шаг -1):
7) 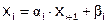 .
.
Метод прогонки корректен при 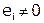 и устойчив при
и устойчив при 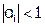 . Достаточное условие, обеспечивающее устойчивость метода:
. Достаточное условие, обеспечивающее устойчивость метода:
 2015-01-07
2015-01-07 825
825








