Метод Зейделя можно рассматривать как модификацию метода Якоби. Основная идея метода состоит в том, чтобы использовать вычисленные компоненты вектора 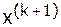 уже на текущей итерации, а не на следующей.
уже на текущей итерации, а не на следующей.
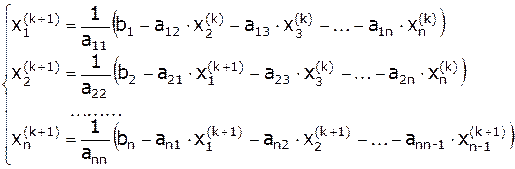
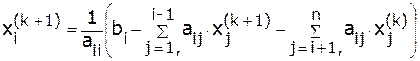
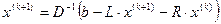
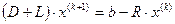
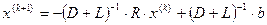 , т.е.:
, т.е.:
 ,
, 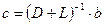 .
.
Система 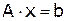 называется нормальной, если матрица
называется нормальной, если матрица 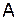 является симметричной и положительно определена, т.е.
является симметричной и положительно определена, т.е. 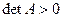 .
.
Достаточный признак сходимости метода Зейделя: если исходная система 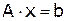 нормальная, то метод Зейделя сходится.
нормальная, то метод Зейделя сходится.
Если исходная система не является нормальной, то ее можно привести к нормальному виду с помощью симметризации Гаусса – путем домножения левой и правой части матричного уравнения на транспонированную матрицу коэффициентов  :
:
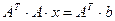 .
.
 2015-01-07
2015-01-07 520
520








