Исходная система 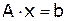 может быть преобразована к эквивалентной системе вида:
может быть преобразована к эквивалентной системе вида:
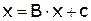 , где
, где
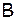 - некоторая новая матрица;
- некоторая новая матрица;
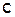 - некоторый новый вектор.
- некоторый новый вектор.
Метод простой итерации (МПИ) предполагает нахождение решения системы 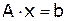 путем вычисления последовательных приближений с помощью рекуррентного равенства:
путем вычисления последовательных приближений с помощью рекуррентного равенства:
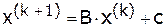 , где
, где
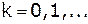 - номер итерации, а
- номер итерации, а 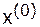 - некоторое начальное приближение. Матрица
- некоторое начальное приближение. Матрица 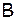 называется матрицей итерирования или перехода.
называется матрицей итерирования или перехода.
Необходимым и достаточным условием сходимости метода простой итерации при любом начальном приближении 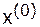 к решению системы
к решению системы 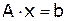 является требование, чтобы все собственные числа матрицы перехода
является требование, чтобы все собственные числа матрицы перехода 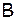 были по модулю меньше 1.
были по модулю меньше 1.
Устойчивый способ разложения 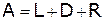 .
.
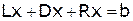
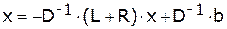
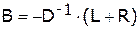 ,
, 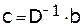
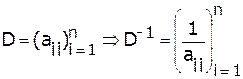
В развернутом виде полученное матричное уравнение можно записать следующим образом:
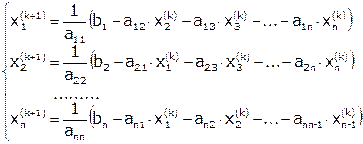
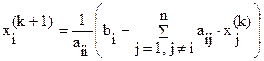
Достаточный признак сходимости метода Якоби.
Метод Якоби сходится в случае диагонального преобладания в матрице коэффициентов СЛАУ:
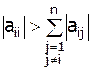 , где
, где 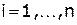 .
.
 2015-01-07
2015-01-07 705
705








