Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке [а, Ь] и имеющую на этом отрезке некоторое число непрерывных производных.
Слово «сплайн» (английское spline) означает гибкую линейку, используемую для проведения гладких кривых: через заданные точки плоскости.
Преимуществом сплайнов перед обычной интерполяцией является, во-первых, их сходимость и, во-вторых, устойчивость процесса вычислений.
Определение. S(x) – сплайн функция, которая соответствует данной функции f(x) и соответственно узлам 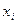 , где i=0..n, и удовлетворяет следующим условиям:
, где i=0..n, и удовлетворяет следующим условиям:
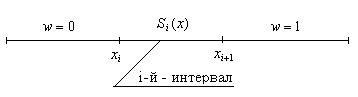
1. На каждом отрезке 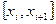 S(x) – является многочленом третьей степени.
S(x) – является многочленом третьей степени.
2.
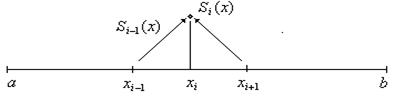 |
S(x) и ее первая и вторая производные непрерывны на заданном интервале [ a,b ].
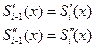
3. В каждом узле значения сплайна равны значениям исходной функции.
 |
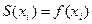
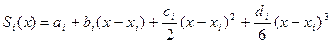
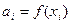 - коэффициенты в узлах
- коэффициенты в узлах
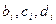 - могут быть определены из условия сшивки.
- могут быть определены из условия сшивки.
Таким образом, можно построить 3n - 2 уравнений, из которых и находят эти коэффициенты. Но необходимо задать еще и условия на границе.
Составим такую форму записи сплайна, которая включает в себя выполнение условия непрерывности самого сплайна и его второй производной.
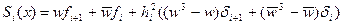
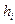 - длина интервала
- длина интервала 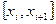
w- относительная координата, которая вычисляется следующим образом
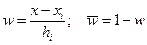
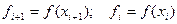
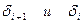 - коэффициенты, которые нужно определить
- коэффициенты, которые нужно определить
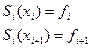
1-я производная:
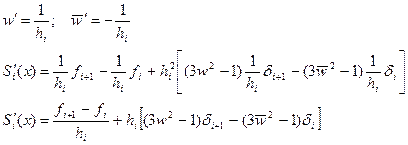
2-я производная:
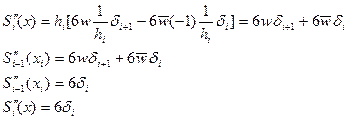
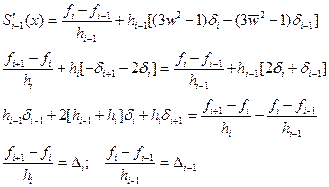
Данное соотношение может быть записано для каждого узла выделенного интервала.
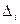 - конечная разность первого порядка.
- конечная разность первого порядка.
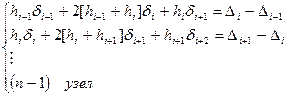
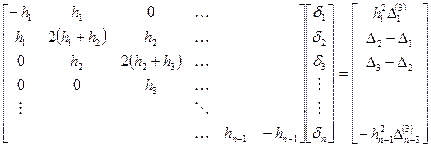
Для крайних верхней и нижней строчек необходимо использовать условия на границе, которые будут иметь следующий вид.
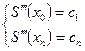
 2015-01-07
2015-01-07 639
639







