Элементы кинематики

Для описания механического движения необходимо указать тело, относительно которого рассматривается движение – тело отсчёта (т.о.). С телом отсчёта связана система координат. Простейшей системой координат является прямоугольная декартова система 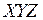(рис.1).

Совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел, называется системой отсчёта.

При движении материальной точки 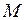(рис.1) конец радиус-вектора 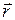описывает в пространстве некоторую линию.

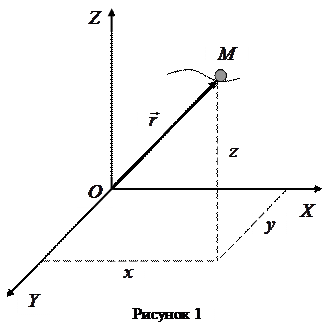
Координаты материальной точки 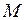при её движении с течением времени изменяются и описываются системой уравнений:

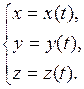(I.1)

Эта система эквивалентна векторному уравнению, называемому законом движения:

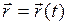. (I.2)

Уравнения (I.1) и (I.2) называются кинематическими уравнениями движения материальной точки.

Наиболее часто пользуются правой прямоугольной декартовой системой координат, изображенной на рис. 2.

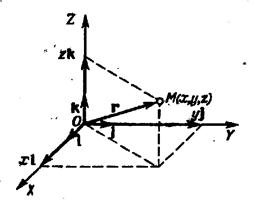
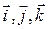- единичные по модулю и взаимно перпендикулярные векторы – орты системы координат, образующие ее ортонормированный базис.

Система координат называется правой, так как из конца третьего орта (вектора 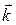) вращение от первого орта (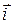) ко второму (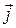) по кратчайшему расстоянию видно происходящим против часовой стрелки, т.е. взаимная ориентация векторов (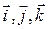) совпадает с взаимной ориентацией трех пальцев правой руки – большого, указательного и среднего, когда они расположены взаимно перпендикулярно. Из правила сложения векторов следует, что радиус-вектор точки М можно разложить по базису 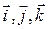следующим образом:

,

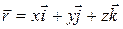где 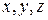- координаты (компоненты) радиуса – вектора 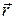относительно базиса;

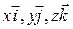- составляющие вектора 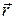по осям координат.

Положение точки в пространстве определяется числом независимых координат, называемых числом степеней свободы.

Рассмотрим частные случаи:

• три степени свободы ( 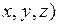- материальная точка свободно движется в пространстве;
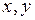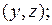
• две степени свободы (); 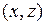- материальная точка движется по некоторой поверхности;
• одна степень свободы 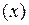, 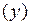или 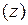- материальная точка движется вдоль некоторой линии.

Траекторией точки называется линия, описываемая этой точкой при ее движении относительно выбранной системы отсчета. Кинематические уравнения движения точки (I.1) задают ее траекторию в параметрической форме. Параметром служит время 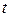. Уравнение траектории точки в обычной форме, т.е. в виде двух уравнений связывающих между собой декартовы координаты точек траектории, можно получить, решая уравнения (I.1) совместно и исключая, из них параметр .

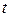Например, пусть кинематические уравнения движения точки заданы в форме:

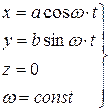
Уравнение траектории этой точки 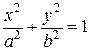, , 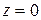т.е. точка движется в плоскости 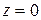по эллиптической траектории с полуосями, равными 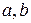. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. Если траектория точки – плоская кривая, т.е. целиком лежит в одной плоскости, то движение точки называют плоским. В общем случае траектория точки представляет собой пространственную кривую.

Простейшими видами механического движения являются поступательное и вращательное движения тела.

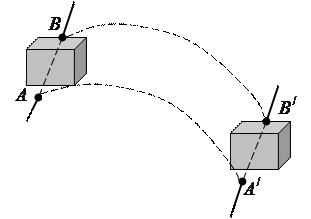
Поступательное движение – это движение, при котором любая прямая, соединяющая две произвольные точк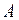и ( и 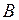) тела, перемещается, оставаясь параллельной самой себе (рис.3).

Например, поступательно движется ящик письменного стола, когда его выдвигают.

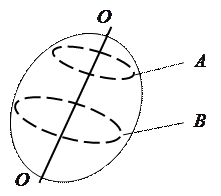Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, перпендикулярной к плоскостям окружностей, называемой осью вращения (ОО) (рис.4).