Как известно, предел числовой последовательности 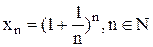 , имеет предел равный e.
, имеет предел равный e. 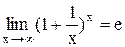 . 1.Пусть
. 1.Пусть 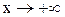 . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами: 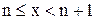 , где n=[x] – это целая часть x. Отсюда следует
, где n=[x] – это целая часть x. Отсюда следует 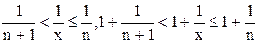 , поэтому
, поэтому 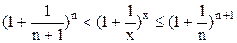 . Если
. Если 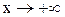 , то
, то 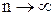 . Поэтому:
. Поэтому: 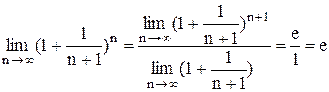 ,
,
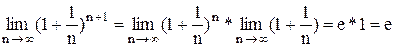 . По признаку существования пределов:
. По признаку существования пределов: 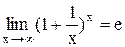 . 2. Пусть
. 2. Пусть 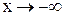 . Сделаем подстановку –x=t, тогда
. Сделаем подстановку –x=t, тогда 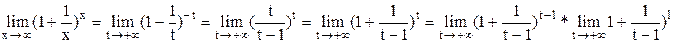 =
= 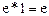 .
. 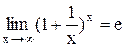 и
и 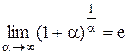 называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция
называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция 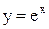 называетсяэкспоненциональной, употребляется также обозначение
называетсяэкспоненциональной, употребляется также обозначение 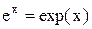 .
.
 2015-01-13
2015-01-13 403
403








