Теорема: если существует 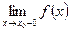 и
и 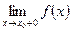 и они равны между собой, то существует
и они равны между собой, то существует 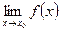 =
= 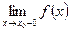
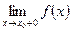 .
.
Теорема: если 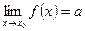 ,
, 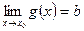 , то =>
, то =>
1) 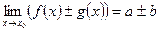
2) 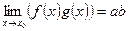
3) 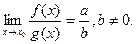
Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть 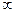 .
.
Примечание 2: 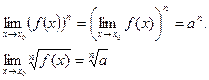
Теорема: если 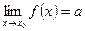 , то функция g(x) = f(x) – a является б.м. при
, то функция g(x) = f(x) – a является б.м. при 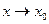 .
.
Следствие: если 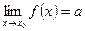 => в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при
=> в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при 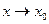 .
.
Теорема: если 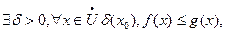 и существуют конечные пределы, когда
и существуют конечные пределы, когда 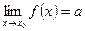 ,
, 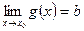 =>
=> 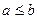 .
.
Теорема (о сжатой переменной): если 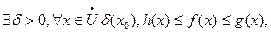 и существуют конечные пределы
и существуют конечные пределы 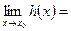
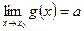 => существует:
=> существует: 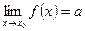 .
.
Теорема (о пределе сложной функции):
Пусть: х0, 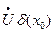 ,U=f(x),
,U=f(x), 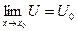 .
.
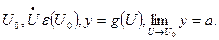
Сама теорема:
Если 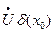 задана сложная функция,
задана сложная функция, 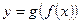 и существуют конечные пределы
и существуют конечные пределы 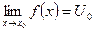 и
и 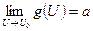 , то
, то 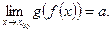
 2015-01-13
2015-01-13 1258
1258








